矩阵方程求解&最小二乘法

矩阵方程的求解主要分为三类

• 超定矩阵方程，m>n,A,b已知
• 盲矩阵方程：b已知，A未知
• 欠定稀疏矩阵方程:m<n，A，b已知但x未知且稀疏

最小二乘法（LS）

普通最小二乘

考虑超定矩阵方程Ax=b,m>n，为了抵制误差对矩阵方程求解的影响，引入一校正向量△b，并用它去“扰动”有误差的数据向量b。我们的目标是，使校正项△b“尽可能小”

$$Ax=b$$

m>n时为超定方程

$$b=b_0+e$$ $$b+\Delta b\to b_0$$

问题可以理解为使

$$||\Delta b||^2\to min$$

的优化问题

$$Ax=b+\Delta b$$ $$L(x)=||Ax-b||_2^2$$ $$=(Ax-b)^H(Ax-b)$$ $$\frac{\partial L(x)}{\partial x^*}=A^HAx-A^Hb=0$$ $$\to x_{LS}=(A^HA)^{-1}A^Hb$$

对于秩亏缺$（rank（A）<n）$的超定方程，最小二乘解为

$$\to x_{LS}=(A^HA)^{\dagger}A^Hb$$

高斯马尔可夫定理

在参数估计理论中,称参数向量$\theta$的估计$\hat{\theta}$为无偏估计，若它的数学期望值等于真实的未知参数向量，即$E{\hat{\theta}}=\theta$。进一步地，如果一个无偏估计还具有最小方差，则称这一无偏估计为最优无偏估计。

类似地，对于数据向量b含有加性噪声或者扰动的超定方程A$\theta$= b+e，若最小二乘解$\theta_{LS}$的数学期望等于真实参数向量$\theta$，便称最小二乘解是无偏的。如果它还具有最小方差，则称最小二乘解是最优无偏的。

高斯马尔科夫定理指出了最优无偏解的条件，对于线性方程组

$$Ax=b_0+e$$

满足

$$\begin{cases} E(e)=0\\ cov\{e\}=E\{ee^H\}=\sigma^2I \end{cases}$$

当且仅当$rank(A)=n$时，最优无偏解为最小二乘解

$$x_{LS}=(A^HA)^{-1}A^Hb$$

LS解与最大似然解的等价性

若加性误差向量$e=[e_1,… ,e_m]^T$为独立同分布的复高斯随机向量,其概率密度函数为

$$f(e)=\frac{1}{\pi^m||_e}exp[-(e-ue)^H(e-Ue)]$$ $$max \log f(e) ==\frac{1}{\sigma^2}e^He$$ $$max f(e) ==min||Ax-b||_2^2$$

所以在高斯马尔科夫条件下，矩阵方程的最大似然解等价于最小二乘解，但误差向量方程不同时，两者不相等

$$\hat{x}_{ML}=\hat{x}_{LS}$$

数据最小二乘（DLS）

与普通最小二乘不同，我们假定b无噪声，数据矩阵$A=A_0+E$有噪声,我们加入校正矩阵$\Delta A$对A进行校准

$$\begin{array}{l} A=A_0+E \\ (A+\Delta A)x=b \end{array}$$

我们的问题变为

$$min||\Delta A||_F^2,s.t.(A+\Delta A)x=b$$

我们采用拉格朗日乘子法进行求解

$$L(x)=||\Delta A||_F^2+\lambda^H(Ax+\Delta Ax-b)$$ $$=tr(\Delta A\Delta A^H)+\lambda^H(Ax+\Delta A x-b)$$ $$\frac{\partial L(x)}{\partial \Delta A^T}=(\Delta A^H)+x\lambda^H=0$$ $$\to \Delta A=-\lambda x^H$$

代入约束条件

$$(A+\Delta A)x=b$$ $$-\lambda x^Hx+Ax=b$$ $$\lambda x^Hx=Ax-b$$ $$\lambda=\frac{Ax-b}{x^Hx}$$ $$\Delta A=-\frac{Ax-b}{x^Hx}x^H$$ $$J(x)=||\Delta A||_F^2$$ $$=tr(\frac{(Ax-b)(Ax-b)^H}{x^Hx})=\frac{||Ax-b||_2^2}{||x||_2^2}$$

得到数据最小二乘

$$\hat{x}_{DLS}=\arg\min_x\frac{(AX-b)^H(Ax-b)}{x^Hx}$$

求导问题

x为一个列向量

• 行向量求偏导 $$\frac{\partial}{\partial x^T}=[\frac{\partial}{\partial x_1},...,\frac{\partial}{\partial x_n}]$$
• 列向量 $$\frac{\partial}{\partial x^T}=[\frac{\partial}{\partial x_1},...,\frac{\partial}{\partial x_n}]^T$$
• example $$\frac{\partial (a^Tx)}{\partial x^T}=a^T$$ $$\frac{\partial (a^Tx)}{\partial x}=a$$
• 矩阵求导 $$L=tr(\Delta A\Delta A^H)+\lambda^H(Ax+\Delta A-b)$$ $$\frac{\partial L}{\partial \Delta A^T}=\Delta A^H+x\lambda^H=0$$

Tikhonov 正则化方法

因为在真实问题中往往存在秩亏缺，所以在最小二乘的代价函数的基础上我们进行改进，加入了正则化参数，在神经网络的代价函数经常用到

$$J(x)=min_{x}||Ax-b||_2^2+\lambda||x||_2^2$$ $$J(x)=x^HA^HAx-x^HA^Hb-b^HAx+b^Hb+\lambda x^Hx$$ $$\frac{\partial J(x)}{\partial x^*}=A^HAx-A^Hb+\lambda x=0$$ $$\to (A^HA+\lambda I)x=A^Hb$$ $$\hat{x}_{Tik}=(A^HA+\lambda I)^{-1}A^Hb$$

这种使用$(A^HA+\lambda I)^{-1}$代替协方差矩阵的直接求逆$(A^HA)^{-1}$的方法常称为Tikhonov正则化(Tikhonov regularization)，或简称正则化方法(regularized method)。

Tikhonov正则化方法的本质是:通过对秩亏缺的矩阵A 的协方差矩阵 $A^HA$ 的每一个对角元素加一个很小的扰动$\lambda$，使得奇异的协方差矩阵$A^HA$ 的求逆变成非奇异矩阵$(A^HA+\lambda I)$的求逆，从而大大改善求解秩亏缺矩阵方程 Ax = b 的数值稳定性。

反正则化去燥

显然，若数据矩阵A 满列秩，但存在误差或者噪声时，就需要采用与Tikhonov正则化相反的做法，对被噪声污染的协方差矩阵$A^HA$ 加一个很小的负扰动矩阵$-\lambda I$，

$$min_x ||Ax-b||_2^2-\lambda||x||_2^2$$ $$\to \hat{x}=(A^HA-\lambda I)^{-1}A^Hb$$

总体最小二乘(TLS)

在A，b同时存在误差的最小二乘方法

$$A=A_0+E$$ $$b=b_0+e$$ $$min||\Delta A,\Delta b||_F^2$$

我们的约束优化问题转化为了

$$min||\Delta A,\Delta b||_2^2=||\Delta A||_2^2+||\Delta b||_2^2,s.t.(A+\Delta A)x=b+\Delta b$$ $$([A,b]+[\Delta A,\Delta b])\begin{bmatrix} x\\ 1 \end{bmatrix}=0$$

令

$$A'=[A,b]$$ $$\Delta A'=[\Delta A,\Delta b])$$ $$x'=\begin{bmatrix} x\\ 1 \end{bmatrix}$$

原方程转化为数据最下二乘问题

$$(A'+\Delta A')x'=0$$ $$\to min_{x'}\frac{(A'x'-b')(A'x'-b')^H}{x'^Hx'}$$ $$=min\frac{x^{'H}A'^HA'x'}{x'^Hx'}$$ $$=min\frac{||Ax-b||_2^2}{||x||_2^2+1}$$

令

$$B=[A,b]$$

其奇异值分解为

$$B=U\Sigma V^H$$

总体最小二乘的解为

$$x'=-\frac{1}{v(n+1,n+1)}V_{min}$$

总体最小二乘的几何意义

和点到线的距离相似$ai^T$是矩阵的第i行，$b_i$是第i个元素，总体最小二乘的解$x{TLS}$是使

$$min_x\frac{||Ax-b||_2^2}{||x||_2^2+1}=\sum_{i=1}^n\frac{|a_i^Tx-b_i|^2}{x^Tx+1}$$

问题转化为了点集$(a_i,b_i)$到直线$b=ax$的最小距离平方和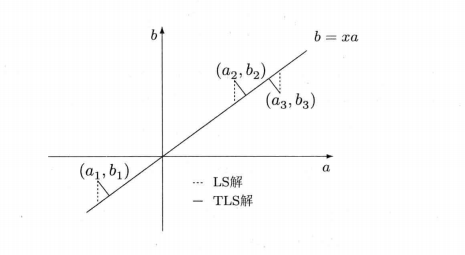

的极小化变量

总体最小二乘闭式解

若增广矩阵$B=[A ,b]$的奇异值为$\sigma1≥…\sigma{n+1}$，则总体最小二乘解可表示成

$$x_{TLS}=(A^HA-\sigma^2_{n+1}I)^{-1}A^Hb$$

与Tikhonov 正则化比较知，总体最小二乘是一种反正则化方法，可以解释为一种具有噪声清除作用的最小二乘方法:先从协方差矩阵 $A^TA$中减去噪声影响项$\sigma_{n+1}^2I$，然后再矩阵求逆，得到最小二乘解。

四种最小二乘的比较

优化目标

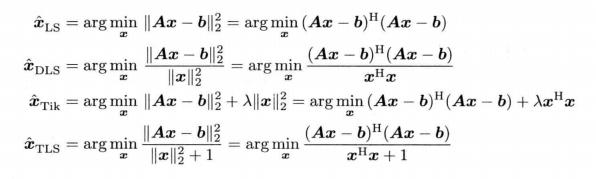
对应解

$$\begin{array}{l} \hat{x}_{LS}=(A^HA)^{-1}A^Hb\\ \hat{x}_{Tik}=(A^HA+\lambda I)^{-1}A^Hb\\ \hat{x}_{TLS}=(A^HA-\sigma^2_{n+1}I)^{-1}A^Hb \end{array}$$

总体最小二乘拟合直线

普通最小二乘考虑拟合误差平方和最小化,对于直线$m(x-\bar x)+(y-\bar y)=0$，代价函数为

$$\begin{array}{l} D_{LS}^{(1)}=\sum_{i=1}^n[(x_i-\bar{x})+m(y_i-\bar{y})]^2 \\ D_{LS}^{(2)}=\sum_{i=1}^n[m(x_i-\bar{x})-(y_i-\bar{y})]^2 \end{array}$$

对于若干数据点集，我们用直线ax+by+c=0拟合，，总体最小二乘考虑数据点距离平方和的最小化

$$D_{TLS}=\frac{\sum_{i=1}^n[a(x_i-\hat{x})+b(y_i-\hat{y})]^2}{a^2+b^2}$$

我们把D转化为单位向量t与M的乘积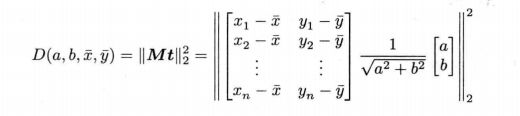

对此，我们有定理，单位法向量$t=(a^2+b^2)^{-1/2}[a,b]^T$取矩阵$M^tM$的最小特征值$\lambda{min}$对应的特征向量，距离平方和取最小值$\lambda{min}$

$$D_{TSL}=\frac{(Mt)^TMt}{||t||_2^2}=\frac{t^TM^TMt}{||t||_2^2}$$

example

对于三个数据点(2,1),(2,4),(5,1)

$$\begin{array}{l} \bar{x}=\frac{1}{3}(2+2+5)=3 \\ \bar{y}=\frac{1}{3}(1+4+1)=2 \end{array}$$ $$M=\begin{bmatrix} 2-3&1-2\\ 2-3&4-2\\ 5-3&1-2 \end{bmatrix} =\begin{bmatrix} -1&-1\\ -1&2\\ 2&-1 \end{bmatrix}$$ $$M^TM= \begin{bmatrix} 6&-3\\ -3&6\\ \end{bmatrix} =\begin{bmatrix} \frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\\ -\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}} \end{bmatrix}\begin{bmatrix} 9&0\\ 0&3 \end{bmatrix}\begin{bmatrix} \frac{1}{\sqrt{2}}&-\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}} \end{bmatrix}$$

所以法向量$t=[1/\sqrt{2},1/\sqrt{2}]^T$
得到拟合直线为

$$\frac{1}{\sqrt{2}}(x-3)+\frac{1}{\sqrt{2}}(y-2)=0$$

距离平方和为

$$D_{TLS}=3$$

如果采用普通最小二乘

$$D_{LS}^{(1)}=\frac{1}{m^2+1}\sum_{i=1}^n[(x_i-\bar{x})+m(y_i-\bar{y})]^2$$ $$\frac{\partial D_{LS}^{(1)}}{\partial m}=6m-3=0$$

平均约束的总体最小二乘

$$[A,b] \begin{bmatrix} x\\-1 \end{bmatrix}=0 \to Cx=0$$

考虑存在于增广矩阵中的噪声矩阵

$$D=[E,e]$$

引入校正矩阵,矩阵中每个列向量都与向量u相关

$$\Delta C=[G_1u,G_2u...G_{n+1}u]\in R^{m\times(n+1)}$$

我们的问题转化为了约束优化问题

$$\min_{u,x}u^TWu$$ $$s.t. (A+\Delta A)x=b+\Delta b$$ $$[\Delta A,\Delta b]=[G_1u,G_2u...G_{n+1}u]$$

W为加权矩阵，通常为对角矩阵，或者单位矩阵

$$min||u||_2^2$$