优化理论

实变量函数无约束优化的梯度分析

松弛序列:称序列 ${ak}{k=0}^{\infty},a_{k+1}

我们通过迭代求解优化问题的过程中，需要产生一个松弛序列

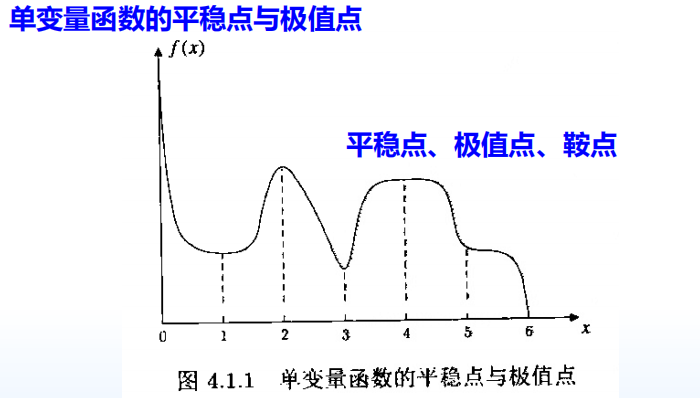
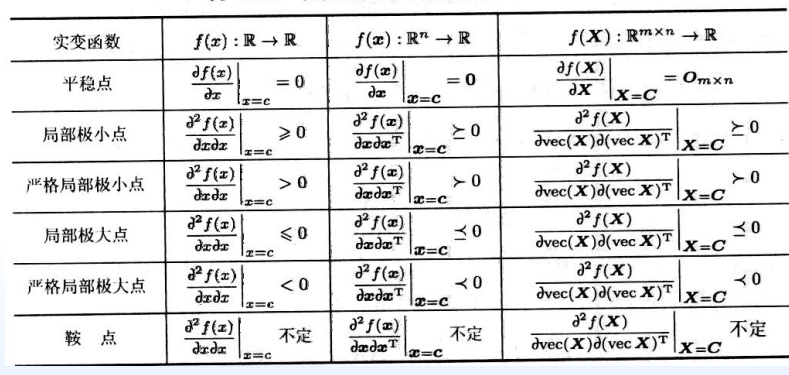
单变量函数的平稳点和极值点

• 全局极小点
• 严格全局极小点
• 开邻域
• 闭邻域

• 极值点
• 平稳点
• 鞍点
  

无约束最小化问题的梯度分析

给定一个实值目标函数

对于超定矩阵方程$Az=b$定义误差平方和

$$J(z)=||Az-b||_b^b=(Az-b)^H(Az-b)$$ $$\frac{\partial J}{\partial z}=z^HA^HAz-z^HA^Hb-b^HAz+b^Hb$$ $$A^HAz-A^Hb=0$$ $$\to z=(A^HA)^{-1}A^Hb$$

曲率

标量$p^HHp$则称为函数f沿着方向p

在无约束最小化问题中，我们常用共轭梯度向量的负方向$-\nabla_{z^*}f(z)$作为更新方向

$$z_k=z_{k-1}-\mu\nabla_{z^*}f(z),\mu>0$$

凸优化理论

最陡下降法(SDA)

$$\nabla x_k=-\nabla f(x_k)$$ $$x_{k+1}=x_k-\mu_k\nabla f(x_k)$$

牛顿法

$$\nabla x_k=-(\nabla^2f(x_k))^{-1}\nabla f(x_k)$$ $$x_k=x_{k-1}-\mu_k(\nabla^2 f(x_{k-1}))^{-1}\nabla f(x_{k-1})$$ $$H=\nabla^2 f(X)$$ $$(\nabla^2 f(x_k))^{-1}\nabla f(x_k) =\Delta x_k$$

• 修正牛顿法 $$（\nabla^2 f(x)+EI）\Delta x=\nabla f(x)$$

  梯度步长的选择$\mu_k$，可以是固定，也可以是不断衰减，比如$\mu_k=\frac{h}{\sqrt{k+1}}$

次梯度法

对于梯度部分不存在的函数,比如y=|x|,(x=0)

$$x_k=x_{k-1}-u\nabla_xf(x_{k-1})$$

f(x)的泰勒展开为

$$f(x+\Delta x)\approx f(x)+(\nabla f(x))^T\Delta x+(\Delta x)^TH\Delta x$$

我们的目的是找到一个次梯度向量g，使其满足

$$f(y)>=f(x)+g^T(y-x)$$

比如

$$f(x)=|x|$$ $$g_i=\begin{cases} 1&x_i>0\\ -1&x_i<0\\ [-1,1]&x_i=0 \end{cases}$$ $$x_k=x_{k-1}-ug(x_{k-1})$$ $$=x_{k-1}-\frac{u}{||g(x_{k-1})||_2}g(x_{k-1})$$

约束优化算法

Lagrangian乘子法

• 优化目标 $$min f(x)$$
• 约束条件 $$s.t. Ax=b$$ 我们可以定义代价函数 $$L(x,\lambda)=f(x)+\lambda^T(Ax-b)$$ 对x，$\lambda$分别求偏导 $$\begin{cases} \frac{\partial L}{\partial x}=0 \\ \frac{\partial L}{\partial \lambda}=Ax-b=0 \end{cases}$$ 更新法则为 $$\begin{cases} x_{k+1}=argmin L(x,\lambda_k)\\ \lambda_{k+1}=\lambda_k-\mu\nabla_{\lambda}L(x_k,\lambda_k) \end{cases}$$

罚函数法

通过罚函数，将约束优化问题变成反映目标函数和约束标间的合成函数的无约束极小化

考虑约束优化问题

$$\min f_0(x)$$ $$s.t. f_i(x)>=0$$ $$h_j(x)=0$$

$x\in F$,F表示x的可行集

加性罚函数

$$L(x)=f_0(x)+p(x)$$ $$\begin{cases} p(x)=0&x\in F \\ p(x)>0&x\in F \end{cases}$$

乘性罚函数

$$L(x)=f_0(x)p(x)$$ $$\begin{cases} p(x)=1&x\in F \\ p(x)>1&x\in F \end{cases}$$

等式约束下罚函数定义

$$p(x)=||h(x)||_2^2=\sum_{i=1}^q|h_i(x)|^2$$

可以看出p(x)具有以下性质

$$p(x)=\begin{cases} =0& h_i(x)=0,i=1,...,q\\ >0& h_i(x)=0,i=1,...,q \end{cases}$$

对于满足等式约束条件的x无影响，对于违背约束条件的点给予惩罚

不等式约束

对于不等式约束

• 外罚函数

  $$P(x)=\sum_i^m(max\{0,-f_i(x)\})^r$$

  外罚函数对于在可行集外部的所有点进行处罚

• 内罚函数

  $$p(x)=\sum_{i=1}^m\frac{1}{f_i(x)}$$

  或

  $$P(x)=\sum_{i=1}^m\frac{1}{f_i(x)}\log|f_i(x)| \\ P(x)=\sum\frac{1}{f_i(x)^p} \\ P(x)=\sum exp(\frac{1}{f_i(x)r})$$

  这种罚函数相当于在可行集边界 bnd(F)上树立起一道围墙，对于企图从可行内集 int(F)穿越到可行集边界 bnd(F)的点 a进行阻挡,故称为内罚函数(interior penalty function),也称障碍函数(barrier function)。

混合罚函数

等式和不等式约束优化的混合罚函数法

混合外罚

$$\min_x f_0(x)+\rho_1\sum(\max\{0,f_i(x)\})^2 +\rho_2\sum|h_j(x)|^2$$

混合内罚

$$\min_x f_0(x)+\rho_1\frac{1}{-f_i(x)}|\log(-f_i(x)|+\rho_2\sum |h_j(x)|^2$$

增广拉格朗日乘子法

Lagrangian乘子法的主要缺点

• 只有当约束优化问题具有局部凸结构时，对偶的无约束优化问题才是良好定义的，并且 Lagrangian乘子的更新$\lambda_{k+1}=\lambda_k +a_kh(x_k)$才有意义。
• Lagrangian目标函数的收敛比较费时，因为 Lagrangian乘子的更新是一种上升迭代(ascent iteration)，只能适度地快速收敛。

罚函数法的不足

• 收敛慢，大的惩罚参数容易引起转化后的无约束优化问题的病态，从而造成算法的数值不稳定性。

拉格朗日和罚函数的结合

等式约束优化Lagrangian乘子法

$$J_P(x,\lambda)=f_0(x)+\lambda^Th(x)+P\psi(h(x))$$ $$\begin{cases} x_k=x_{k-1}+\Delta x&-\mu\nabla_x L(x,\lambda)|_{x_{k-1},\lambda_{k-1}}\\ \lambda_k=\lambda_{k-1}+\Delta \lambda&-\mu\nabla_x L(x,\lambda)|_{x_{k-1},\lambda_{k-1}} \end{cases}$$

混合约束优化Lagrangian乘子法

对于优化问题

$$\min_xf(x) s.t.Ax=b,Bx<=b$$

令非负向量s>=0，为松弛变量，使得Bx+s=h,将问题转化为等式约束

$$L_p(x,s,\lambda,v)=f(x)+\lambda^T(Ax-b)+V^H(Bx+s-h)+\rho(||Ax-b||_2^2+||Bx+s-h||_2^2)$$