Maxwell’s Theory

maxwell’s Equations

微分形式麦克斯韦方程组

$$\begin{cases} \nabla\times\overrightarrow{E}=\frac{\partial}{\partial t}\overrightarrow{B},\\ \nabla\times\overrightarrow{H}=\frac{\partial}{\partial t}\overrightarrow{D}+\overrightarrow{J},\\ \nabla\cdot\overrightarrow{B}=0,\\ \nabla\cdot\overrightarrow{D}=\rho \end{cases}$$

• 1为法拉第定律或法拉第磁感应定律。
• 2为安培定律或广义安培电路定律式
• 3为电场的库仑定律或高斯定律。
• 4为高斯定律或磁场的高斯定律。

物质本构方程

$$\bar D=\epsilon_0\bar E$$ $$\bar B=\mu_0 \bar H$$

其中

$$\epsilon_0=8.85\times10^{-12} F/m$$ $$\mu_0=4\pi\times10^{-7} H/m$$

Vector Analysis

向量运算重要公式

$$\bar C\cdot (\bar A\times \bar B)=\bar A\cdot (\bar B\times \bar C)=\bar B\cdot (\bar C\times \bar A)$$ $$\bar C\times (\bar A\times \bar B)=\bar A(\bar C\cdot \bar B)-(\bar C\cdot \bar A)\bar B$$

$\nabla$:del Operatoe(del 算符)

定义

$$\nabla=\hat{x}\frac{\partial}{\partial x}+\hat{y}\frac{\partial}{\partial y}+\hat{z}\frac{\partial}{\partial z}$$

重要公式

$$\nabla \cdot(\bar E\times \bar H)=\bar H \cdot(\nabla \times \bar E)-\bar E \cdot(\nabla \times \bar H)$$ $$\nabla\cdot(\nabla \times \bar A)=0$$ $$\nabla \times(\nabla \phi)=0$$ $$\nabla \times(\nabla\times\bar E)=\nabla(\nabla\cdot\bar E)-\nabla^2\bar E$$

Laplaceian Operator（拉普拉斯算符）

$$\nabla^2=\nabla\cdot\nabla=\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}+\frac{\partial^2}{\partial z^2}$$

Gradient 梯度

$$\nabla\phi=\hat{x}\frac{\partial}{\partial x}\phi+\hat{y}\frac{\partial}{\partial y}\phi+\hat{z}\frac{\partial}{\partial z}\phi$$

Divergence 散度

$$\nabla\cdot\bar D=\frac{\partial}{\partial x}D_x+\frac{\partial}{\partial y}D_y+\frac{\partial}{\partial z}D_z$$

通量是单位时间通过某个曲面的量，散度是通量的强度和流量

Curl 旋度

$$\nabla\times\bar D=\hat{x}(\frac{\partial}{\partial y}H_z-\frac{\partial}{\partial z}H_y) +\hat{y}(\frac{\partial}{\partial z}H_x-\frac{\partial}{\partial x}H_z)+\hat{z}(\frac{\partial}{\partial x}H_y-\frac{\partial}{\partial y}H_x)$$

1.2电磁波

Wave Equation and Wave Solution(波动方程和波动解)

微分形式的麦克斯韦方程对空间中的每一点都是有效的。为了解出这个方程，我们将从研究在无源区域的麦克斯韦方程组的解开始。

$$\begin{cases} \nabla\times\overrightarrow{E}=-\mu_0\frac{\partial}{\partial t}\overrightarrow{H},\\ \nabla\times\overrightarrow{H}=\epsilon_0\frac{\partial}{\partial t}\overrightarrow{H},\\ \nabla\cdot\overrightarrow{E}=0,\\ \nabla\cdot\overrightarrow{H}=0 \end{cases}$$

两边同取旋度

$$\nabla\times\nabla\times\bar E=-\mu_0\epsilon_0\frac{\partial^2}{\partial t^2}\bar E$$

亥姆霍兹方程

$$\nabla^2\bar E-\mu_0\epsilon_0\frac{\partial^2}{\partial t^2}\bar E=0$$

满足该方程的解为波动解

---

对于该偏微分方程，最简单的解为电场方向在x方向，传播方向只延z方向的波

$$\bar E=\hat{x}E_x(z,t)$$ $$\bar E=\hat{x}E_0cos(kz-wt)$$

其中

$$k^2=w^2\mu_0\epsilon_0$$

该关系称为色散关系

dispersion relation:色散关系

色散关系提供了空间频率k和时间频率w之间的重要联系

在研究时空变化量，如E(z,t)时，有两种观点。时间的观点是研究不同时间在空间中固定点上的变化。空间视角是研究固定时间的空间变化。

重要关系

$$f=\frac{w}{2\pi}=\frac{k}{\sqrt{\mu_0\epsilon_0}}=kc$$ $$c=\frac{w}{k}$$

对应磁场解

$$\bar H=\hat{y}E_0\frac{1}{\eta_0}cos(kz-wt)$$

其中
$\frac{1}{\eta_0}=\sqrt{\frac{\epsilon_0}{\mu_0}}$,$\eta$为自由空间阻抗

Unit for Spatial Frequence k

$$k=\frac{2\pi}{\lambda}$$

k的单位定义为$K_0$

$$K_0=2\pi rad/m$$

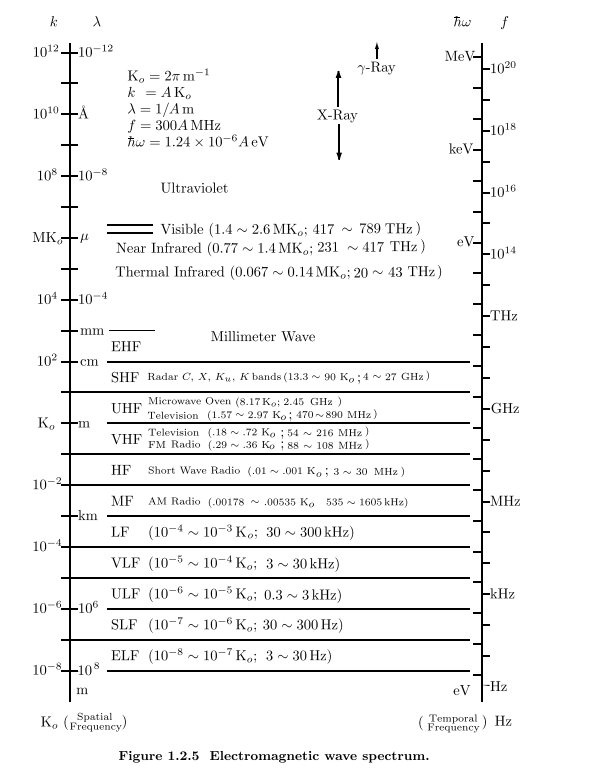
电磁波谱

相速度

$$v_p=\frac{dz}{dt}=\frac{w}{k}=\frac{1}{\sqrt{\mu_o\epsilon_0}}$$

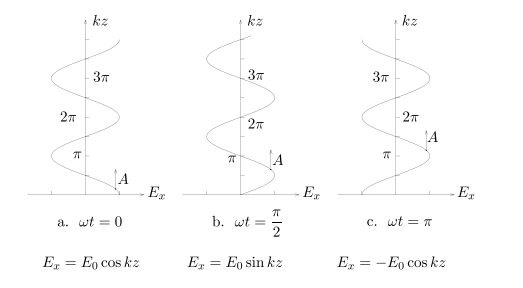
相速度可以理解为图中A点移动的速度，相位的传播，在真空中等于光速

相位延迟

$$A_p=\frac{k}{w}=\sqrt{\mu_o\epsilon_0}$$

Polarization极化

对于波动方程解

$$\bar E(z,t)=\hat{x}E_x+\hat{y}E_y$$ $$=\hat{x}cos(kz-wt)+\hat{y}Acos(kz-wt+\phi)$$

从时间域看

• 线性极化

$\phi=2m\pi$,$\phi=(2m+1)\pi$

$$\bar E(z,t)=\hat{x}cos(wt)\pm\hat{y}Acos(wt)$$

• 圆极化
  $\phi=\pi/2,A=1$ $$\bar E(z,t)=\hat{x}cos(wt)+\hat{y}sin(wt)$$
• 椭圆极化
  $\phi=\pi/2$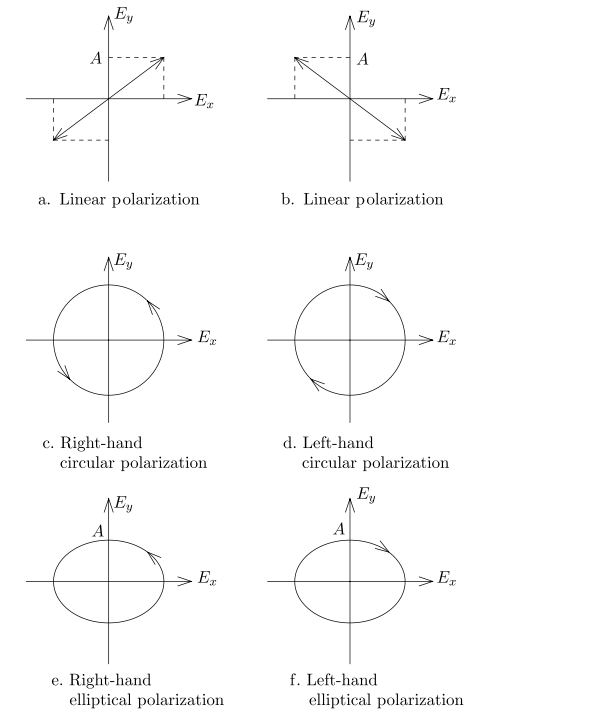 $$\bar E(z,t)=\hat{x}cos(wt)+\hat{y}Asin(wt)$$

  $\phi=+\pi/2$右旋，
  $\phi=-\pi/2$左旋

$0<\phi<\pi$右旋，
$\pi<\phi=2\pi$左旋

空间角度看极化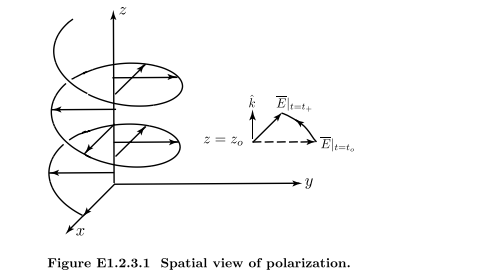

Herztian Waves 赫兹天线

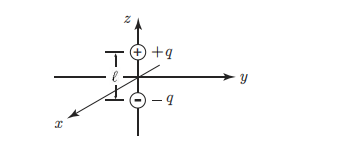
一个赫兹偶极子是由两个相对的电荷($\pm q$)组成，它们之间隔着无穷小的距离。偶极矩p= ql有一个角频率w，使得每个点电荷在2$\pi$/w的周期内从+q变化到-q。p被定义为$l→0与q→无穷$的乘积，使p为常数。假设两个电荷位于z=±l/2处。赫兹解出了所有的电磁场用势函数称为赫兹势$\Pi$

$$\Pi=\frac{ql}{4\pi r}cos(kr-wt)$$

• $kr\gg1$ $$\bar E=-\hat{\theta}\frac{k^2ql}{4\pi\epsilon_0r}sin\theta cos(kr-wt)$$ $$\bar H=-\hat{\phi}\frac{wkql}{4\pi\epsilon_0r}sin\theta cos(kr-wt)$$
• $w=0$ $$\bar E=\frac{ql}{4\pi\epsilon_0r^3}(\hat{\theta}sin\theta+\hat{r}2cos\theta)$$ $$\bar H=0$$
• 在偶极子附近 $$\bar H=\hat{\phi}\frac{wql}{4\pi r^2}sin\theta$$

Constitutive Relations 物质本构关系

Isotropic Media各向同性介质

$$\bar D=\epsilon \bar E$$ $$\bar B=\mu\bar H$$

Anisotropic Media各向异性介质

$$\bar D=\bar \epsilon \bar E$$ $$\bar B=\bar \mu\bar H$$

Bianisotropic Media双各向异性介质

$$\bar D=\bar \epsilon \bar E+\bar \xi\bar H$$ $$\bar B=\bar\zeta\bar E+ \bar \mu\bar H$$

Biisotropic Media手性介质

$$\bar D= \epsilon \bar E+\tau\bar H$$ $$\bar B=\tau\bar E+ \mu\bar H$$

Boundary Condition边界条件

$$\hat{n}\cdot(\bar{E_1}-\bar{E_2})=0$$ $$\hat{n}\cdot(\bar{H_1}-\bar{H_2})=\bar J_s$$ $$\hat{n}\cdot(\bar{B_1}-\bar{B_2})=0$$ $$\hat{n}\cdot(\bar{D_1}-\bar{D_2})=\rho_s$$