KDB

wave vector k的引入

由亥姆霍兹方程

$$(\nabla^2+w^2\mu\epsilon)\overrightarrow{E}=0$$

解得

$$\overrightarrow{E}(\overrightarrow{r})=\overrightarrow{E}e^{i(k_xx+k_yy+k_zz)}$$ $$k_x^2+k_y^2+k_z^2=w^2\mu\epsilon=k^2$$

定义wave vector k

$$\overrightarrow{k}=\hat{x}k_x+\hat{y}k_y+\hat{z}k_z$$

position vector

$$\overrightarrow{r}=\hat{x}x+\hat{y}y+\hat{z}z$$

则

$$\overrightarrow{k}\cdot\overrightarrow{r}=k_xx+k_yy+k_zz$$

则

$$\overrightarrow{E}(\overrightarrow{r})=\overrightarrow{E}e^{i\overrightarrow{k}\cdot\overrightarrow{r}}$$

代回麦克斯韦方程

$$\begin{cases} \overrightarrow{k}\times\overrightarrow{E}=w\mu\overrightarrow{H}\\ \overrightarrow{k}\times\overrightarrow{H}=-w\epsilon\overrightarrow{E}\\ \overrightarrow{k}\cdot\overrightarrow{E}=0\\ \overrightarrow{k}\cdot\overrightarrow{H}=0 \end{cases}$$

波印廷矢量

$$\overrightarrow{S}=\frac{1}{2}Re \begin{cases}\frac{\overrightarrow{k}}{w\epsilon}|\overrightarrow{H}|^2\\\frac{\overrightarrow{k^*}}{w\mu^*}|\overrightarrow{E}|^2 \end{cases}$$

k矢量的意义

• 波是平面波
• 波的方向确定
• $k=2\pi/\lambda$可以计算波长，频率

  KDB坐标系

对于平面波

$$\overrightarrow{k}\times\overrightarrow{E}=w\overrightarrow{B}$$ $$\overrightarrow{k}\times\overrightarrow{H}=-w\overrightarrow{D}$$ $$\overrightarrow{k}\cdot\overrightarrow{B}=0 \overrightarrow{k}\cdot\overrightarrow{D}=0$$

可得k垂直于BD构成的平面，BD不一定互相垂直，EH也不一定在BD平面内(垂直：perpendicular)

定义三个单位向量$\hat{e_1},\hat{e_2},\hat{e_3}$,$\hat{e_3}$和k方向相同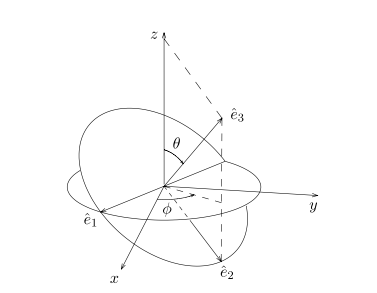

转换矩阵（将xyz坐标系转换到KDB坐标系）

$$\bar{T}=\begin{bmatrix} sin\varPhi&-cos\varPhi&0，\\ cos\theta cos\varPhi&cos\theta sin\varPhi&-sin\theta\\ sin\theta cos\varPhi&sin\theta sin\varPhi &cos\theta \end{bmatrix}$$ $$\bar{T}^{-1}=\begin{bmatrix} sin\varPhi&cos\theta cos\varPhi&sin\theta cos\varPhi\\ -cos\varPhi&cos\theta sin\varPhi&sin\theta sin\varPhi\\ 0&-sin\theta&cos\theta \end{bmatrix}$$

对于任意矢量

$$\overrightarrow{A}= \begin{bmatrix} A_x\\ A_y\\ A_z \end{bmatrix}$$ $$\overrightarrow{A_k}= \begin{bmatrix} A_1\\ A_2\\ A_3 \end{bmatrix}$$

存在

$$\overrightarrow{A_k}=\bar{T}\cdot\overrightarrow{A}$$

对于任意场量

$$\overrightarrow{E}=\bar\kappa\cdot\overrightarrow{D}+\bar\chi\cdot\overrightarrow{B}$$ $$\overrightarrow{H}=\bar\nu\cdot\overrightarrow{B}+\bar\gamma\cdot\overrightarrow{D}$$ $$\overrightarrow{D}=\bar\epsilon\overrightarrow{E}+\bar\xi\overrightarrow{H}$$ $$\overrightarrow{B}=\bar\mu\overrightarrow{H}+\bar\zeta\overrightarrow{E}$$

转化为KDB坐标系

$$\overrightarrow{E}=(\bar{T}\cdot\bar\kappa\cdot \bar{T}^{-1})\cdot\overrightarrow{D}+(\bar{T}\cdot\bar\chi\cdot \bar{T}^{-1})\cdot\overrightarrow{B}$$ $$\overrightarrow{H}=(\bar{T}\cdot\bar\nu\cdot \bar{T}^{-1})\overrightarrow{D}+(\bar{T}\cdot\bar\gamma\cdot \bar{T}^{-1})\cdot\overrightarrow{B}$$ $$\overrightarrow{D}=(\bar{T}\cdot\bar\epsilon\cdot \bar{T}^{-1})\cdot\overrightarrow{E}+(\bar{T}\cdot\bar\xi\cdot \bar{T}^{-1})\cdot\overrightarrow{H}$$ $$\overrightarrow{B}=(\bar{T}\cdot\bar\mu\cdot \bar{T}^{-1})\cdot\overrightarrow{H}+(\bar{T}\cdot\bar\zeta\cdot \bar{T}^{-1})\cdot\overrightarrow{E}$$

我们可以得到

$$\bar\kappa_k=\bar{T}\cdot\bar\kappa\cdot \bar{T}^{-1}$$ $$\bar\chi_k=\bar{T}\cdot\bar\chi\cdot \bar{T}^{-1}$$ $$\bar\nu_k=\bar{T}\cdot\bar\nu\cdot \bar{T}^{-1}$$ $$\bar\gamma_k=\bar{T}\cdot\bar\gamma\cdot \bar{T}^{-1}$$ $$\bar\epsilon_k=\bar{T}\cdot\bar\epsilon\cdot \bar{T}^{-1}$$ $$\bar\xi_k=\bar{T}\cdot\bar\xi\cdot \bar{T}^{-1}$$ $$\bar\mu_k=\bar{T}\cdot\bar\mu\cdot \bar{T}^{-1}$$ $$\bar\zeta_k=\bar{T}\cdot\bar\zeta\cdot \bar{T}^{-1}$$

在KDB坐标系的物质本构方程

$$\overrightarrow{E}=\bar\kappa_k\cdot\overrightarrow{D}+\bar\chi_k\cdot\overrightarrow{B}$$ $$\overrightarrow{H}=\bar\nu_k\cdot\overrightarrow{D}+\bar\gamma_k\cdot\overrightarrow{B}$$ $$\overrightarrow{D}=\bar\epsilon_k\overrightarrow{E}+\bar\xi_k\overrightarrow{H}$$ $$\overrightarrow{B}=\bar\mu_k\overrightarrow{H}+\bar\zeta_k\overrightarrow{E}$$

为什么引入KDB坐标系？

把微分方程转化为线性方程，讲话运算，解决双各向异性这样最复杂的介质的麦克斯韦方程，将所有的介质归一化

Maxwell Equation in KDB System

下面我们将运用KDB坐标系解决麦克斯韦方程

KDB坐标系麦克斯韦方程组

$$\begin{cases} \overrightarrow{k}\times\overrightarrow{E}_k=w\overrightarrow{B}_k\\ \overrightarrow{k}\times\overrightarrow{H}_k=-w\overrightarrow{D}_k\\ \overrightarrow{k}\cdot\overrightarrow{B}_k=0\\ \overrightarrow{k}\cdot\overrightarrow{D}_k=0 \end{cases}$$

由

$$\overrightarrow{k}\cdot\overrightarrow{B}_k=0\\ \overrightarrow{k}\cdot\overrightarrow{D}_k=0$$

知

$$B_3,D_3=0$$

因为

$$\bar k=\hat{e_3}k$$

所以

$$w\bar B_k=k\hat{e_3}\times(\hat{e_1}E_1+\hat{e_2}E_2+\hat{e_3}E_3)$$ $$-w\bar D_k=k\hat{e_3}\times(\hat{e_1}H_1+\hat{e_2}H_2+\hat{e_3}H_3)$$

全部转化为DB的线性方程

$$wB_2=kE_1=k(\kappa_{11} D+\kappa_{22} D+\chi _{11}B+\chi_{12} B)$$ $$wB_1=kE_2=-k(\kappa_{21} D+\kappa_{22} D+\chi_{21} B+\chi_{22} B)$$ $$wD_2=-kH_1=-k(\nu_{11}B_1+\nu_{12}B_2+\gamma_{11}D_1+\gamma_{12}D_2)$$ $$wD_1=-kH_2=-k(\nu_{21}B_1+\nu_{22}B_2+\gamma_{21}D_1+\gamma_{22}D_2)$$

令u=w/k
移项可以化简为

$$\begin{pmatrix} \kappa_{11}&\kappa_{22}\\ \kappa_{21}&\kappa_{22} \end{pmatrix} \begin{pmatrix} D_1,\\ D_2 \end{pmatrix}=- \begin{pmatrix} \chi_{11}&\chi_{12}-u\\ \chi_{21}+u&\chi_{22} \end{pmatrix} \begin{pmatrix} B_1,\\ B_2 \end{pmatrix}$$ $$\begin{pmatrix} \nu_{11}&\nu_{22}\\ \nu_{21}&\nu_{22} \end{pmatrix} \begin{pmatrix} B_1,\\ B_2 \end{pmatrix} =-\begin{pmatrix} \gamma_{11}&\gamma_{12}+u\\ \gamma_{21}-u&\gamma_{22} \end{pmatrix} \begin{pmatrix} D_1,\\ D_2 \end{pmatrix}$$

可以得到均匀介质色散关系

各向同性介质中的波

现在用KDB坐标系去推导最简单的介质，各向同性介质的麦克斯韦方程

$$\bar E=\kappa\bar D$$ $$\bar H=\nu\bar B$$

在KDB坐标系下

$$\bar E_k=\kappa\bar D_k$$ $$\bar H_k=\nu\bar B_k$$

代入KDB矩阵方程

$$\kappa \begin{pmatrix} D_1\\ D_2 \end{pmatrix}= \begin{pmatrix} 0&u\\ -u&0 \end{pmatrix} \begin{pmatrix} B_1\\ B_2 \end{pmatrix}$$ $$\nu \begin{pmatrix} B_1\\ B_2 \end{pmatrix} =\begin{pmatrix} 0&-u\\ u&0 \end{pmatrix} \begin{pmatrix} D_1\\ D_2 \end{pmatrix}$$

消去B得到

$$\begin{pmatrix} u^2-\kappa\nu&0\\ 0&u^2-\kappa\nu \end{pmatrix} \begin{pmatrix} D_1,\\ D_2 \end{pmatrix}=0$$

解得

$$u^2-\kappa\nu=0$$

• $D_1=D_2=0$
  • 没有场
• $D_ 1 \not= 0, D_2=0$
  • e1方向极化波
• $D_1=0,D_2\not= 0$
  • e2方向极化波
• $D_1\not= 0,D_2\not= 0$
  • 任意方向极化波

Wave in uniaxial Media单各向异性介质

加入磁场后的plasma media，手机通讯

物质本构方程

$$\bar E=\bar\kappa\bar D$$ $$\bar H=\nu\bar B$$

其中

$$\bar\kappa= \begin{pmatrix} \kappa&0&0\\ 0&\kappa&0\\ 0&0&\kappa_z \end{pmatrix}$$ $$\bar\kappa_k=\bar{T}\cdot\bar\kappa\cdot \bar{T}^{-1}= \bar\kappa= \begin{pmatrix} \kappa&0&0\\ 0&\kappa cos^2\theta+\kappa_zsin^2\theta&(\kappa-\kappa_z)sin\theta cos\theta\\ 0&(\kappa-\kappa_z)sin\theta cos\theta&\kappa sin^2\theta+\kappa_zcos^2\theta \end{pmatrix}$$ $$\begin{pmatrix} u^2-\kappa_{11}\nu&0\\ 0&u^2-\kappa_{22}\nu \end{pmatrix} \begin{pmatrix} D_1\\ D_2 \end{pmatrix}=0$$

解得

• $D_1=D_2=0$
  • 没有场
• $D 1 \not= 0, D_2=0，u^2-\kappa{11}\nu=0$
  • e1方向极化波
  • $u=\pm \sqrt{\nu\kappa_{11}}=\pm \sqrt{\nu\kappa}$

$$\bar D_k=\hat{e}_1D_1$$ $$\bar B_k=\hat{e}_2\frac{u}{\nu}D_1$$ $$\bar H_k=\hat{e}_2uD_1$$ $$\bar E_k=\hat{e}_1\kappa D_1$$

• $D1=0,D_2\not=0,u^2-\kappa{22}\nu=0$
  • e2方向极化波
  • $u=\pm \sqrt{\nu\kappa_{22}}=\pm \sqrt{\nu(\kappa cos^2\theta+\kappa_zsin^2\theta)}$

    速度和角度相关，称为非寻常波,相位和k传播方向相反

$$\bar D_k=\hat{e}_2D_2$$ $$\bar B_k=\hat{e}_1\frac{u}{\nu}D_2$$ $$\bar H_k=-\hat{e}_2uD_2$$ $$\bar E_k=\hat{e}_2\kappa_{22} D_2+\hat{e}_3(\kappa-\kappa_{z})sin\theta cos\theta D_2$$

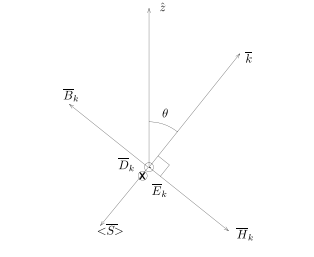
• $D1\not=0,D_2\not=0,u^2-\kappa{11}\nu=u^2-\kappa_{22}\nu=0$
  • 则$\kappa{11}=\kappa{22}$,不满足

双折射现象

当电磁波进入单轴介质中时，将会分解为两种速度不同的线性极化特征波，分别对应2,3两种情况

wave in Gyrotropic Media 陀螺介质中的波

物质本构方程

$$\bar E=\bar\kappa\bar D$$ $$\bar H=\nu\bar B$$

其中

$$\bar\kappa= \begin{pmatrix} \kappa&ik_g&0\\ -ik_g&\kappa&0\\ 0&0&\kappa_z \end{pmatrix}$$ $$\bar\kappa_k=\bar{T}\cdot\bar\kappa\cdot \bar{T}^{-1}= \bar\kappa= \begin{pmatrix} \kappa&ik_gcos\theta&ik_gsin\theta\\ -ik_gcos\theta&\kappa cos^2\theta+\kappa_zsin^2\theta&(\kappa-\kappa_z)sin\theta cos\theta\\ ik_gsin\theta&(\kappa-\kappa_z)sin\theta cos\theta&\kappa sin^2\theta+\kappa_zcos^2\theta \end{pmatrix}$$ $$\begin{pmatrix} u^2-\kappa\nu&-i\nu\kappa_gcos\theta\\ i\nu\kappa_gcos\theta&u^2-\nu(\kappa cos^2\theta+\kappa_zsin^2\theta) \end{pmatrix} \begin{pmatrix} D_1\\ D_2 \end{pmatrix}=0$$

Faraday Rotation

当波向z方向传播时，$\theta$=0

$$\begin{pmatrix} u^2-\kappa\nu&-i\nu\kappa_g\\ i\nu\kappa_g&u^2-\nu\kappa \end{pmatrix} \begin{pmatrix} D_1\\ D_2 \end{pmatrix}=0$$

我们得到

$$\frac{D_2}{D_1}=\frac{u^2-\nu\kappa}{i\nu\kappa_g}=-\frac{i\nu\kappa_g}{u^2-\nu\kappa}$$ $$u^2-\nu\kappa=\pm\nu\kappa_g$$ $$u=w/k=\sqrt{\nu(\kappa\pm\kappa_g)}$$ $$\frac{D_2}{D_1}=\pm i$$

波可以分解为两个垂直的线性极化波，所以波为圆极化波

• 左旋

$$k^{I}=w/\sqrt{\nu(\kappa+\kappa_g)}$$ $$\frac{D_2}{D_1}=-i$$ $$\bar D=\hat{e_1}D_1-i\hat{e_2}D_1$$ $$=\bar D_R+iD_I$$

• 右旋

$$k^{II}=w/\sqrt{\nu(\kappa-\kappa_g)}$$ $$\frac{D_2}{D_1}=i$$

当线性极化波$\bar D=\hat{e}_12D_0$,z的正方向入射该介质时，将波分解成

$$\bar D=D_0(\hat{e}_1+\hat{e}_2i)+D_0(\hat{e}_1-\hat{e}_2i)$$

假设介质厚度为d

$$\bar D=D_0(\hat{e}_1+\hat{e}_2i)e^{ik^Iz}+D_0(\hat{e}_1-\hat{e}_2i)e^{ik^{II}z}$$ $$=\hat{e}_1D_0(e^{i\Phi_I}+e^{i\Phi_{II}})+\hat{e}_2D_0(e^{i\Phi_I}-e^{i\Phi_{II}})$$ $$\Phi_I=k^Iz_0=\frac{wz_0}{\sqrt{v(\kappa+\kappa_g)}}$$ $$\Phi_{II}=k^Iz_0=\frac{wz_0}{\sqrt{v(\kappa-\kappa_g)}}$$ $$\frac{D_2}{D_1}=i\frac{e^{i\Phi_I}-e^{i\Phi_{II}}}{e^{i\Phi_I}+e^{i\Phi_{II}}}=-tan\frac{\Phi_{II}-\Phi_I}{2}$$

经过该介质后线极化波方向发生改变，称为法拉第旋转，z方向+负号

Wave in Bianisotropic Media

$$\bar E= \begin{pmatrix} \kappa&0&0\\ 0&\kappa&0\\ 0&0&\kappa_z \end{pmatrix} \cdot\bar D +\begin{pmatrix} \chi&0&0\\ 0&\chi&0\\ 0&0&\chi_z \end{pmatrix} \cdot\bar B$$ $$\bar H= \begin{pmatrix} \gamma&0&0\\ 0&\gamma&0\\ 0&0&\gamma_z \end{pmatrix} \cdot\bar D +\begin{pmatrix} \nu&0&0\\ 0&\nu&0\\ 0&0&\nu_z \end{pmatrix} \cdot\bar B$$

其中

$$\bar\kappa_k=\bar{T}\cdot\bar\kappa\cdot \bar{T}^{-1}= \bar\kappa= \begin{pmatrix} \kappa&0&0\\ 0&\kappa cos^2\theta+\kappa_zsin^2\theta&(\kappa-\kappa_z)sin\theta cos\theta\\ 0&(\kappa-\kappa_z)sin\theta cos\theta&\kappa sin^2\theta+\kappa_zcos^2\theta \end{pmatrix}$$

Chiral Media（手性介质）

$$\overrightarrow{E}=\kappa\overrightarrow{D}-i\chi\overrightarrow{B}$$ $$\overrightarrow{B}=i\chi\overrightarrow{D}+\nu\overrightarrow{B}$$ $$\frac{D_2}{D_1}=\frac{u^2-\nu\kappa+\chi^2}{2i\chi\mu}=-\frac{2i\chi\mu}{u^2-\nu\kappa+\chi^2}$$ $$u=\sqrt{\nu\kappa}\pm\chi$$ $$\frac{D_2}{D_1}=\pm i$$

• 左旋

$$k^{I}=w/(\sqrt{\nu\kappa}+\chi)$$ $$\frac{D_2}{D_1}=-i$$

• 右旋

$$k^{II}=w/(\sqrt{\nu\kappa}-\chi)$$ $$\frac{D_2}{D_1}=i$$

当线性极化波$\bar D=\hat{e}_12D_0$入射该介质时，将波分解成

$$\bar D=D_0(\hat{e}_1+\hat{e}_2i)+D_0(\hat{e}_1-\hat{e}_2i)$$

假设介质厚度为d

$$\bar D=D_0(\hat{e}_1+\hat{e}_2i)e^{ik^Iz}+D_0(\hat{e}_1-\hat{e}_2i)e^{ik^{II}z}$$ $$=\hat{e}_1D_0(e^{i\Phi_I}+e^{i\Phi_{II}})+\hat{e}_2D_0(e^{i\Phi_I}-e^{i\Phi_{II}})$$ $$\Phi_I=k^Iz_0=\frac{wz_0}{\sqrt{\nu\kappa}+\chi}$$ $$\Phi_{II}=k^Iz_0=\frac{wz_0}{\sqrt{\nu\kappa}-\chi}$$ $$\to \frac{D_2}{D_1}=i\frac{e^{i\Phi_I}-e^{i\Phi_{II}}}{e^{i\Phi_I}+e^{i\Phi_{II}}}=-tan\frac{\Phi_{II}-\Phi_I}{2}$$

optical activity:旋光性，旋光性和法拉第旋转有本质区别

重点归纳

如何解任意介质的麦克斯韦方程？

1. 根据物质本构关系确定对于KDB坐标系下的本构关系 $$\bar{T}=\begin{bmatrix} sin\varPhi&-cos\varPhi&0\\ cos\theta cos\varPhi&cos\theta sin\varPhi&-sin\theta\\ sin\theta cos\varPhi&sin\theta sin\varPhi &cos\theta \end{bmatrix}$$ 2.代入以下矩阵方程

$$\begin{pmatrix} \kappa_{11}&\kappa_{22}\\ \kappa_{21}&\kappa_{22} \end{pmatrix} \begin{pmatrix} D_1\\ D_2 \end{pmatrix}=- \begin{pmatrix} \chi_{11}&\chi_{12}-u\\ \chi_{21}+u&\chi_{22} \end{pmatrix} \begin{pmatrix} B_1\\ B_2 \end{pmatrix}$$ $$\begin{pmatrix} \nu_{11}&\nu_{22}\\ \nu_{21}&\nu_{22} \end{pmatrix} \begin{pmatrix} B_1\\ B_2 \end{pmatrix} =-\begin{pmatrix} \gamma_{11}&\gamma_{12}+u\\ \gamma_{21}-u&\gamma_{22} \end{pmatrix} \begin{pmatrix} D_1\\ D_2 \end{pmatrix}$$

3.分类讨论

• 反对角元素为0直接解方程
• 反对角元素不为0用D1，D2之比解方程