Media
3.1time-harmonic field 正弦时变场
信号频域分析
基本公式
作用,去除麦克斯韦方程中微分,把微分方程化为代数方程
频域麦克斯韦
推导
频域麦克斯韦方程组
频域亥姆霍兹方程
极化(Polarization of Monochromatic Waves)
对于$\overrightarrow{E}(\overrightarrow{r},t)$当r=0,令频域
由$\overrightarrow{E}_R$,$\overrightarrow{E}_I$定义的的平面称为极化平面
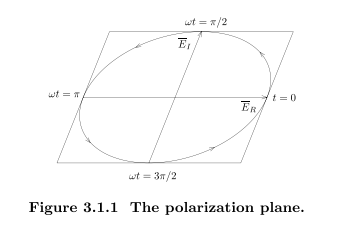
当$E_R,E_I$平行时,波线性极化,垂直时圆极化或椭圆极化
频域功率计算
定义频域波印廷矢量
定义
可得
同理
所以频域波印廷矢量
时域波印廷矢量
代入得
在2$\pi$的时间内时域波印廷矢量的平均值
> 计算时域能量可以用频域公式去除积分,化简运算
Conducting media介质中的波
在导电介质中,根据欧姆定律
$\overrightarrow{J}_c$为欧姆电流,$\overrightarrow{J}_f$为传导电流
由
令
当没有自由电流时得
取电场只有x方向最简单的解$\overrightarrow{E}=\hat{x}\overrightarrow{E}=\hat{x}\overrightarrow{E}_0e^{ikz}$
解得
频域电场强度
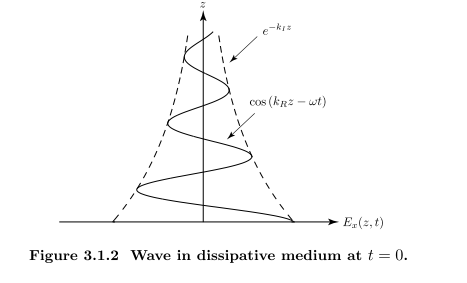
转化为时域
可以看出波沿传导方向指数衰减
定义穿透深度
当波衰减为0时刻的1/e
根据频率,介质特性分两种情况,系数定义为损耗正切
- $1<<\frac{\sigma}{w\varepsilon}$ 一般取0.1
- 导电能力弱
- 穿透深度大
- $1>>\frac{\sigma}{w\epsilon}$ 一般取10
- 导电能力强
- 穿透深度小
Plasme Media中的波
等离子体介质由自由电子和正离子构成,存在极化电场$\overrightarrow{P}$
,因为离子体电子速度v远小于光速c
定义
得到亥姆霍兹方程
根据$w_p$的大小,有两种解
- $w>w_p$
- $w<w_p$
按指数衰减而不传播时间平均功率的波称为倏逝波。在全反射章节中会再次出现,全反射时的透射波也是倏逝波,不传播能量
phase and group velocities相速度和群速度
当$w>w_p$
令$w_1=w_0+\delta w$,$w_2=w_0-\delta w$
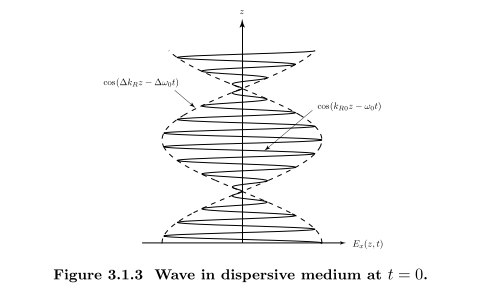
两个波线性叠加,形成驻波
定义
phase velocity=w/k
group velocity=$\frac{1}{\partial k/\partial w}$
则$v_p=\frac{w}{k}=\frac{c}{\sqrt{1-w_p^2/w^2}}>c$
$v_g=\frac{1}{\partial k/\partial w}=c\sqrt{1-w_p^2/w^2}<c$
$v_gv_p=c^2$
相速度可以理解为简谐波在传播的过程中固定相位的点沿着波传播方向上的速度,例如,波峰的传播速度或者波谷的传播速度,也就是波长除以周期。这个概念比较好形象的解释。群速度可以解释为振幅值的变化的传播速度(对于简谐振动,我们可以理解为群速度不存在。因为不存在振幅值的变化,更别提这个变化的传播了。所以群速度都是针对非简谐振动而言的。对于折射系数大于1的介质,相速度大于群速度,对于折射系数小于1的介质,相速度小于群速度(反常介质,不存在)
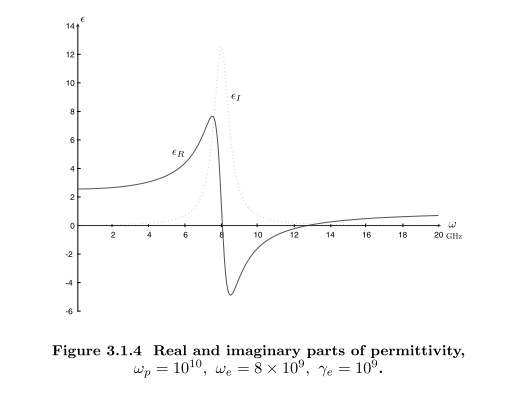
Dispersive Media
亥姆霍兹方程
化简得