Reflection and Transmission

界面处场的关系

$$\hat{n}\times(\bar{E}_1-\bar{E}_2)=0$$ $$\hat{n}\times(\bar{H}_1-\bar{H}_2)=\bar{J}_s$$ $$\hat{n}\cdot(\bar{B}_1-\bar{B}_2)=0$$ $$\hat{n}\cdot(\bar{D}_1-\bar{D}_2)=0$$

任何圆极化和椭圆极化可以分解为两个线性极化波TE,TM波求解

Js为界面处电荷密度

为了解决反射和透射问题，我们把波分为两组类型，TE波和TM波，因为任何波都可以用着两种波线性组合

Reflection and Transmission of TE Waves

电场场垂直入射平面的波，垂直极化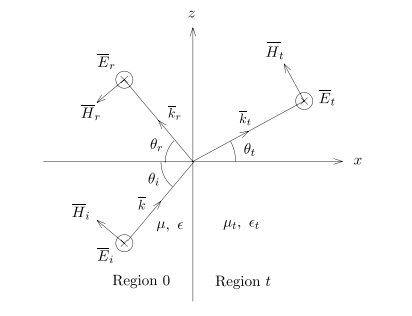

incidence wave 入射波

$$\bar{k}_i=\hat{x}k_x+\hat{z}k_z$$ $$\bar{E}_i=\hat{y}e^{i\bar{k}_i\cdot\bar{r}}$$ $$\bar{H}_i=\frac{1}{w\mu}\bar k_i\times\bar E_i$$ $$\bar S_i=\bar k_i\frac{1}{w\mu}|\bar E_i|^2$$

Reflected Wave 反射波

$$\bar{k}_r=\hat{x}k_x+\hat{z}k_z$$ $$\bar{E}_r=\hat{y}Re^{i\bar{k}_r\cdot\bar{r}}$$ $$\bar{H}_r=\frac{1}{w\mu}\bar k_r\times\bar E_r$$ $$\bar S_r=\bar k_r\frac{1}{w\mu}|\bar E_r|^2$$

Transmission Wave透射波

$$\bar{k}_t=\hat{x}k_x+\hat{z}k_z$$ $$\bar{E}_t=\hat{y}Te^{i\bar{k}_t\cdot\bar{r}}$$ $$\bar{H}_i=\frac{1}{w\mu}\bar k_t\times\bar E_t$$ $$\bar S_i=\bar k_t\frac{1}{w\mu}|\bar E_t|^2$$

反射界面关系

$$\hat{y}e^{i\bar{k}_i\cdot\bar{r}}+\hat{y}Re^{i\bar{k}_r\cdot\bar{r}}=\hat{y}Te^{i\bar{k}_t\cdot\bar{r}}$$

令x=0

$$e^{k_{iz}z}+Re^{k_{rz}z}=Te^{k_{tz}z}$$

对于任意z成立

相位连续方程

$$k_{iz}=k_{rz}=k_{tz}$$

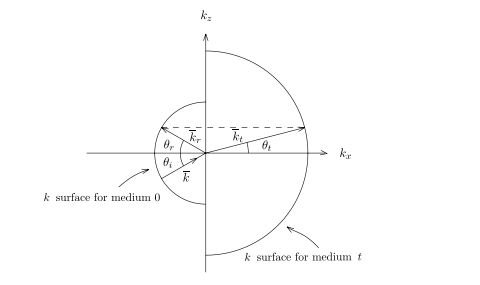
相位连续方程phase matching condition代表入射波和折射波反射波的切向分量是连续的

$$k_isin\theta_i=k_rsin\theta_r=k_tsin\theta_t$$ $$\theta_i=\theta_r$$ $$\sqrt{\mu\epsilon}sin\theta_i=\sqrt{\mu_t\epsilon_t}sin\theta_t$$ $$n_isin\theta_i=n_tsin\theta_t$$ $$\frac{sin\theta_i}{sin\theta_t}=\frac{k_t}{k_i}=\frac{n_t}{n_i}$$

斯涅耳定理Snell’s law

$$n_t=c\sqrt{\mu_t\epsilon_t}$$

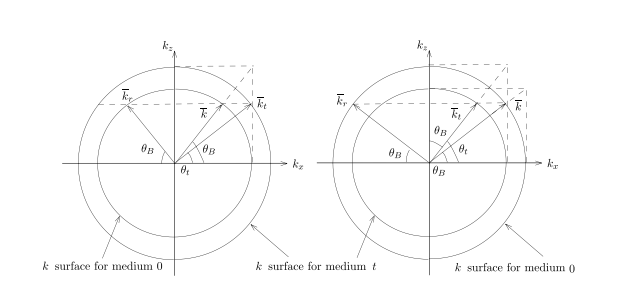
所以在之后解决折射问题可以利用相位连续方程画出k surface图直接解决

上述方程化简后

$$1+R=T$$

为了求解上述二元方程，还需要另一个方程，利用界面处磁场关系（无电流情况）

$$\frac{1}{w\mu}k_{ix}e^{k_{iz}z}+\frac{1}{w\mu}Rk_{rx}e^{k_{rz}z}=\frac{1}{w\mu_t}k_{tx}e^{k_{tz}z}$$ $$\frac{k_x}{\mu}(1-R)=\frac{k_{tx}}{\mu_t}T$$

联立1+R=T

$$\begin{cases} R=\frac{1-p_{0t}}{1+p_{0t}}\\ T=\frac{2}{1+p_{0t}} \end{cases}$$ $$p_{0t}=\frac{\mu k_{tx}}{\mu_t k_{ix}}$$

$p_{0t}$:Fresnd refletion菲涅尔反射系数,安培的好朋友,这表明折射波和反射波的能量由界面两边的介质和入射角度决定

能量关系

$$<\bar S_i>=\frac{1}{2}Re\{\bar k\frac{1}{w\mu}\}$$ $$<\bar S_r>=\frac{1}{2}Re\{\bar k_r\frac{1}{w\mu}|R|^2\}$$ $$<\bar S_t>=\frac{1}{2}Re\{\bar k_t^*\frac{1}{w\mu_t^*}|T|^2e^{i({k_{tx}-k_{tx}^*)x}}\}$$

Reflection and Transmission of TM Waves

磁场垂直入射平面的波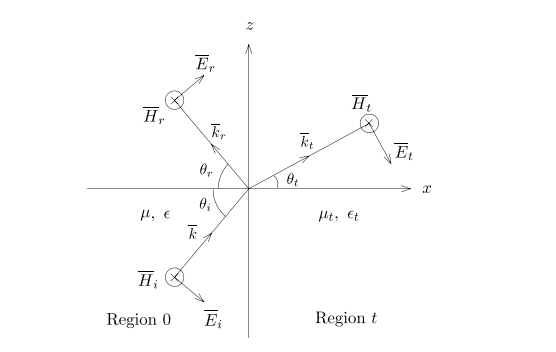

和TE波完全相同，作以下变化

$$E \to H$$ $$H\to E$$ $$\mu\to \epsilon$$

则

$$p_{0t}=\frac{\epsilon k_{tx}}{\epsilon_t k_{ix}}$$

Total Reflection and Critical Angle 全反射和临界角

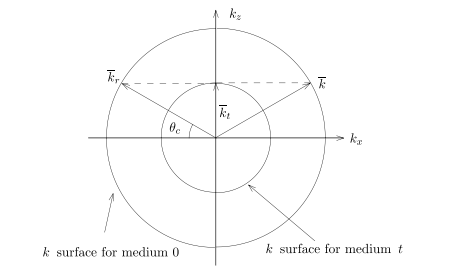
透射光和入射光满足

$$k_isin\theta_i=k_tsin\theta_t$$

临界条件

$$k_isin\theta_c=k_t$$

当

$$k_{iz}>k_t k_{tx}=\sqrt{k_t^2-k_{iz}^2}=ik_{txI}$$

此时

$$\bar E_t=\hat{y}Te^{ik\cdot r}=\hat{y}Te^{-k_{txI}x}e^{ik_zz}$$

得到沿着z方向传播，延x方向衰减的波：倏逝波

能量去哪了？

全反射

$$R=\frac{1-p_{0t}}{1+p_{0t}}=\frac{1-ip_{0tI}}{1+ip_{0tI}}=e^{i2\phi_t}$$ $$\phi_t=-tan^{-1}p_{0tI}=-tan^{-1}\frac{\epsilon k_{txI}}{\epsilon_tk_x}$$ $$T=1+R=2cos\phi_te^{i\phi_t}$$

定义r，t,能量反射系数，能量折射系数

$$r=\frac{s_{rx}}{s_{ix}}$$ $$t=\frac{s_{tx}}{s_{ix}}$$ $$r+t=1$$ $$<S_t(r,t)>=\hat{z}k_z\frac{2cos^2\phi}{w\epsilon_t}e^{-2k_{txI}x}$$

能量只延z方向传播，没有x的分量，为表面波

TE，TM波的另一种说法

perpendicularly polaried wave
垂直极化波
paralally polarized wave，水平极化波

以电场方向为准

Backward Waves and Negative Refraction 反向波和负折射

对于21世纪Media$\mu_t<0,\epsilon_t<0$

这个时候能量如何传播？

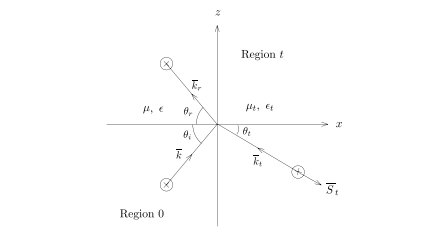
此时k和s的方向相反，即波的传播方向和能量传播方向相反，且入射波和折射波在同一界面

Total Transmission and Brewster Angle全透射和布鲁斯特角

存在全反射波，那么是否存在全透射波？

对于TM波

$$R^{TM}=0$$

则

$$p_{0t}=\frac{\epsilon k_{tx}}{\epsilon_t k_{ix}}=1$$ $$\epsilon k_{tx}=\epsilon_t k_{ix}$$ $$\epsilon k_{t}cos\theta_t=\epsilon_t k_{i}cos\theta_i$$ $$\epsilon w\sqrt{\mu_t\epsilon_t}cos\theta_t=\epsilon_t w\sqrt{\mu\epsilon}cos\theta_i$$ $$k_{i}cos\theta_t= k_{t}cos\theta_i$$

又由

$$k_{iz}=k_{tz}$$ $$k_{i}sin\theta_t= k_{t}sin\theta_i$$

• $\theta_i=\theta_t$

  $$k_i=k_t \epsilon_t=\epsilon$$

  介质相同，全透射

• $\theta_i+\theta_t=\pi$

  $$tan\theta_i=\frac{k_t}{k_i}=\sqrt{\frac{\epsilon_t}{\epsilon}} \theta_i=tan^{-1}\frac{k_t}{k_i}$$

  布鲁斯特角和全反射角区别

$$\theta_C=sin^{-1}\frac{k_t}{k_i} \theta_B=tan^{-1}\frac{k_t}{k_i}$$

Double Refraction in Uniaxial Media 双折射

对于k in uniaxial media

$$k^e=\frac{w}{\sqrt{v(\kappa cos^2\theta+\kappa_zsin^2\theta)}}$$ $$k^o=\frac{w}{\sqrt{\nu\kappa}}$$

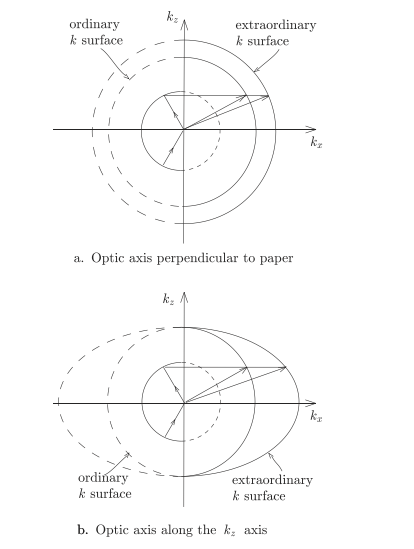
光轴旋转后？

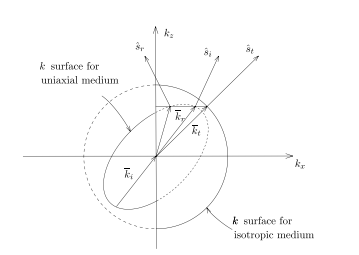
Reflection and Transmission by a Layered Medium 多层介质的折射和反射

下面推导TM波的情况

Regiom #0

$$\bar H_0=\bar H_i+\bar H_r$$ $$=\hat{y}(e^{i(k_{0x}x+k_zz)}+Re^{i(k_{rx}x+k_zz)})$$ $$\bar k_i=\hat{x}k_{0x}+\hat{z}k_z$$ $$k_{0x}^2+k_z^2=k_0^2=w^2\mu_0\epsilon_0$$ $$\bar k_r=-\hat{x}k_{0x}+\hat{z}k_z$$ $$\bar E_0=-\frac{1}{w\epsilon_0}[\hat zk_{0x}e^{i(k_{0x}x+k_zz)}-\hat{z}k_{0x}Re^{i(-k_{0x}x+k_zz)} -\hat{x}k_ze^{i(k_{0x}x+k_zz)}-\hat{x}k_zRe^{i(-k_{0x}x+k_zz)}]$$

Regiom #l

$$\bar H_l =\hat{y}(A_le^{i(k_{lx}x+k_zz)}+B_le^{i(k_{lx}x+k_zz)})$$ $$\bar E_l=-\frac{1}{w\epsilon_0}[\hat z A_lk_{lx}e^{i(k_{lx}x+k_zz)} -\hat{z}k_{lx}B_le^{i(-k_{lx}x+k_zz)} -\hat{x}A_lk_ze^{i(k_{lx}x+k_zz)}-\hat{x}k_zB_le^{i(-k_{lx}x+k_zz)}]$$

At x=dl

$$A_le^{ik_{lx}d_l}+B_le^{-ik_{lx}d_l} =A_{l+1}e^{ik_{(l+1)x}d_{l}}+B_{l+1}e^{-ik_{(l+1)x}d_{l}}$$ $$A_le^{ik_{lx}d_l}-B_le^{-ik_{lx}d_l} =p_{l(l+1)}[A_{l+1}e^{ik_{(l+1)x}d_{l}}+B_{l+1}e^{-ik_{(l+1)x}d_{l}}]$$ $$p_{l(l+1)}=\frac{\epsilon_l k_{(l+1)x}}{\epsilon_{l+1}k_{lx}}$$

列出每层边界的方程，求解

用矩阵表示

$$\begin{bmatrix} A_{l+1}\\ B_{l+1} \end{bmatrix} = \bar V_{(l+1)l}\cdot \begin{bmatrix} A_{l}\\ B_{l} \end{bmatrix} = \frac{1+P_{(l+1)l}}{2} \begin{bmatrix} e^{-i(k_{(l+1)x}-k_{lx})d_l}& R_{(l+1)l}e^{-i(k_{(l+1)x}+k_{lx})d_l}\\ R_{(l+1)l}e^{i(k_{(l+1)x}+k_{lx})d_l} &e^{i(k_{(l+1)x}-k_{lx})d_l} \end{bmatrix} \cdot \begin{bmatrix} A_{l+1}\\ B_{l+1} \end{bmatrix}$$