Wave Guide

Guidance by Conducting Parrallel Plates 金属波导

导引

对于一个非常非常导电的conducting Media$\epsilont=\epsilon_g+i\sigma/w,\sigma/w\epsilon_g>>1$

此时TE波的菲涅尔反射系数$P{ot}^{TE}=\infty,R^{TE}=-1,T^{TE}=0$

$$\bar{E}_1=\bar E_i+\bar E_r=\hat{y}(2isink_{ix}x)e^{ik_zz}$$ $$\bar{E}_1(r,t)=-\hat{y}2sink_{ix}xsin(kz-wt)$$

在x方向形成驻波

模型建立

在x=0，x=d电场强度为0的位置放置两块平行板

y方向电场

$$E_y=Ae^{ik_xx+ik_zz}+e^{-ik_xx+ik_zz}$$

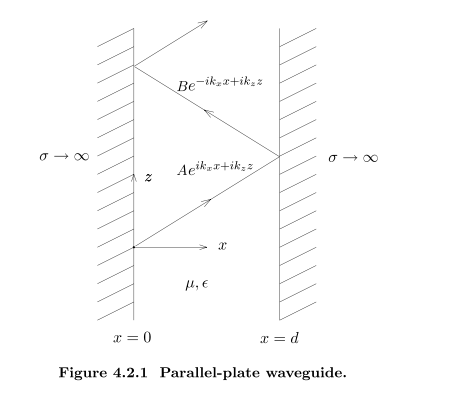
由上述推导知

• 当x=0 $$A/B=-1$$
• 当x=d $$B/A=-e^{i2k_xd}$$

得到

$$e^{i2k_xd}=1=e^{i2m\pi}$$ $$\to 2k_xd=2m\pi$$

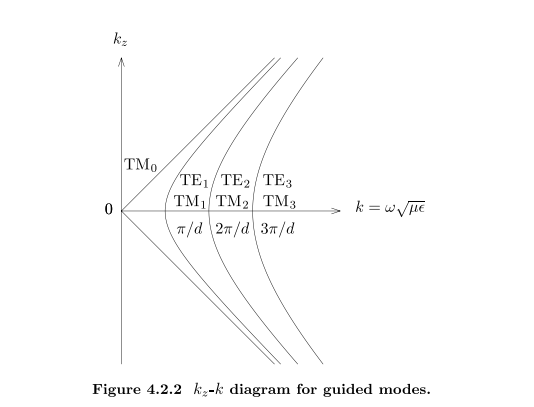
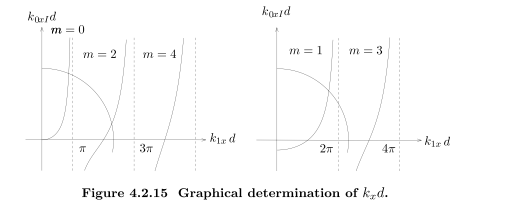
Guidance Condition导波条件

$k_x=\frac{m\pi}{d}=\frac{m}{2d}K_0$

TE波m不可以取0，
TM波m可以取0

物理意义
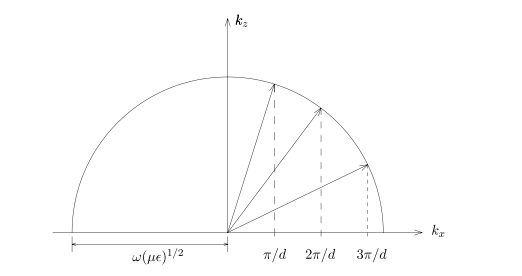
对于一个频率的波，只有特定方向的波可以传播

$k^2_z+(\frac{m\pi}{d})^2=k^2$

当$k<\frac{m\pi}{d}$时，$k_z$为虚数，波将不断衰减，无法传播

$$m<\frac{dw\sqrt{\mu_0\epsilon_0}}{\pi}=\frac{dw}{\pi c}$$

cutoff spatial frequence

$$k_{cm}=\frac{m\pi}{d}=\frac{m}{2d}K_0$$

$k<k_{cm}$时波延z方向指数衰减

$$\lambda<=\lambda=\frac{2\pi}{k_{c1}}=2d$$

只有波长小于2d的波可以传导

对于$\frac{m}{2d}<k<\frac{(m+1)}{2d}$只有m个TE波的模式和m+1个TM波的模式

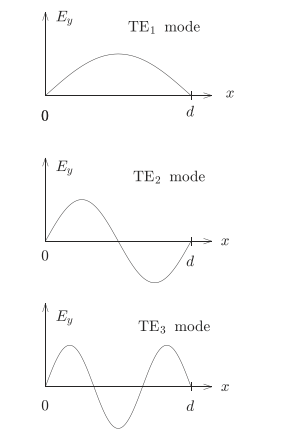
m越小，群速度越大,传递信息量越大，模式越低，传递信息月快

$$v_p=\frac{c}{\sqrt{1-(k_x/k)^2}}$$ $$v_g=c\sqrt{1-(k_x/k)^2}$$

Excitation of Modes in Parrllel-Plate Waveguides平行波导中模的激发

上述推导假设平行板不存在电荷，当波导存在线电流时，$\sigma$不为无穷时，根据边界条件

$$\bar J_s=\hat{y}J_s(x)$$ $$H_x|_{z=0_+}-H_x|_{z=0_-}=J_s(x)$$

由欧姆定律

$$J=\sigma E$$ $$\to E_w=\frac{J}{\sigma}$$ $$H_w=\frac{1}{\eta}E_w$$ $$\eta=\sqrt{\frac{\mu}{\epsilon_m}}$$ $$(\epsilon_m=(\epsilon+i\frac{\sigma}{\epsilon w}))$$ $$\bar{S}=\bar{E}\times\bar{H}^*$$

知金属里出现电场,会有能量向外泄露

TM Modes in Parrallel-Plate Waveguide TM波在波导的传播模式

$$\bar H=\hat{y}\bar H_0(e^{ik_xx+ik_zz}+e^{-ik_xx+ik_zz})$$ $$=\hat{y}2H_0cosk_xxe^{ik_zz}$$ $$\bar{E}=2H_0\frac{1}{w\epsilon}[\hat{x}k_zcosk_xx-\hat{z}k_xsink_xx]e^{ik_zz}$$ $$<S_z>=\frac{k}{2w\epsilon}|H_0|^2$$

当kx=0

$$\bar{H}=\hat{y}H_0e^{ikz}$$ $$\bar{E}=\hat{y}\eta H_0e^{ikz}$$

$\eta$：特性阻抗

Guide Wave in a Symmetric Slab Dielectric Waveguide介质波导

对于TE波

$$\bar E_0=\hat{y}e^{ik_{0x}x}e^{ik_{z}z}$$ $$\bar E_1=\hat{y}(Ae^{ik_{1x}x}e^{ik_{z}z}+e^{-ik_{1x}x}e^{ik_{z}z})$$ $$\bar E_2=\hat{y}e^{ik_{2x}x}e^{ik_{z}z}$$

---

$$p_{10}=\frac{i\mu_1\alpha}{\mu_0k_{0x}}=iP_{10I}$$ $$R_{10}=R_{12}=\frac{1-P_{10}}{1+P_{10}}=e^{i2\phi_{10}}$$

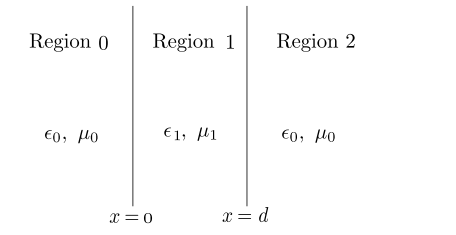
每次反射后都会增加相位

得到导波条件

$$k_{1x}d+2\phi_{10}=m\pi$$ $$\phi=-tan^{-1}(\frac{\mu k_{1xI}}{\mu_1 k_x})$$ $$(k_{1x}d)^2+(k_{0x}d)^2=(k_1^2-k_0^2)d^2$$

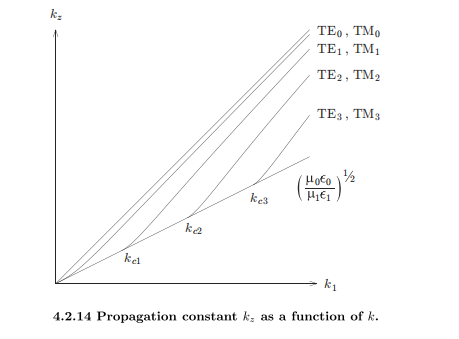
cut off

$$k_1=k_{cm}=\frac{m\pi}{d\sqrt{1-\mu_0\epsilon_0/\mu_1\epsilon_1}}$$

光纤通讯的原理就是介质波导

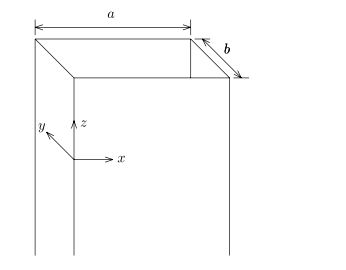
Cylindrical Rectangular Waveguides矩形波导

为了将问题化简，引入一个在xy平面的向量s

$$\bar E=\bar E_s+\hat{z}\bar E_z$$ $$\bar E_s=\hat{x}\bar E_x+\hat{y}\bar E_y$$

定义

$$\nabla=\nabla_s+\hat{z}\frac{\partial}{\partial z}$$

则对于麦克斯韦方程，可以转化为

$$(\nabla_s+\hat{z}\frac{\partial}{\partial z})\times(\bar E_s+\hat{z}\bar E_z)=iw\mu(\bar H_s+\hat{z}\bar H_z)$$ $$(\nabla_s+\hat{z}\frac{\partial}{\partial z})\times(\bar H_s+\hat{z}\bar H_z)=-iw\epsilon(\bar E_s+\hat{z}\bar E_z)$$ $$\to \begin{cases} \nabla_s\times\bar E_s=iw\mu\bar H_z \\ \nabla_s\times\hat{z}\bar E_z+\hat{z}\frac{\partial}{\partial z}\bar \times E_s=iw\mu\bar H_s \\ \nabla_s\times\bar H_s=-iw\mu\bar E_z \\ \nabla_s\times\hat{z}\bar H_z+\hat{z}\frac{\partial}{\partial z}\bar \times H_s=-iw\mu\bar E_s \end{cases}$$ $$\to \begin{cases} \bar E_s=\frac{1}{w^2\mu\epsilon-k_z^2}[\nabla_s\frac{\partial}{\partial z}E_z+iw\mu(\nabla_s\times H_z)] \\ \bar H_s=\frac{1}{w^2\mu\epsilon-k_z^2}[\nabla_s\frac{\partial}{\partial z}H_z-iw\epsilon(\nabla_s\times E_z)] \end{cases}$$

代回原方程

$$(\nabla_s+w^2\mu\epsilon-k_z^2) \begin{bmatrix} E_z\\ H_z \end{bmatrix} =0$$

• $E_z=0,H_z=\not0$

  TE wave

  $$H_z=cosk_xcosk_yye^{ik_zz}$$ $$H_x=\frac{-ik_xk_z}{w^2\mu\epsilon-k_z^2}sink_xxcosk_yye^{ik_zz}$$ $$H_y=\frac{-ik_yk_z}{w^2\mu\epsilon-k_z^2}cosk_xxsink_yye^{ik_zz}$$ $$E_x=\frac{-iw\epsilon k_y}{w^2\mu\epsilon-k_z^2}cosk_xxsink_yye^{ik_zz}$$ $$E_y=\frac{iw\epsilon k_x}{w^2\mu\epsilon-k_z^2}sink_xxcosk_yye^{ik_zz}$$ $$E_z=0$$

---

• $E_z= \not0,H_z=0$

  TM wave

$$E_z=sink_xsink_yye^{ik_zz}$$ $$E_x=\frac{ik_xk_z}{w^2\mu\epsilon-k_z^2}cosk_xxsink_yye^{ik_zz}$$ $$E_y=\frac{ik_yk_z}{w^2\mu\epsilon-k_z^2}sink_xxcosk_yye^{ik_zz}$$ $$H_x=\frac{-iw\epsilon k_y}{w^2\mu\epsilon-k_z^2}sink_xxcosk_yye^{ik_zz}$$ $$H_y=\frac{iw\epsilon k_x}{w^2\mu\epsilon-k_z^2}cosk_xxsink_yye^{ik_zz}$$ $$H_z=0$$

波导条件

$$k_xa=m\pi$$ $$k_yb=n\pi$$ $$(\frac{m\pi}{a})^2+(\frac{n\pi}{b})^2+k_z^2=k^2$$

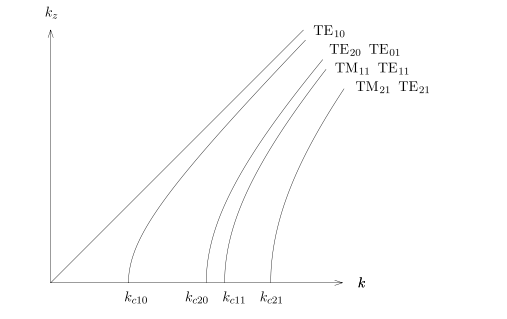
cut off spatial frequence

$$k_{cmn}=\sqrt{(m\pi/a)^2+(n\pi/b)^2}$$

Cylindrical Circular Waveguides圆柱波导

Bessel Function

把亥姆霍兹方程化为柱坐标系

$$(\nabla_s+w^2\mu\epsilon-k_z^2) \begin{bmatrix} E_z\\ H_z \end{bmatrix} =0$$ $$\to (\frac{1}{\rho}\frac{\partial}{\partial\rho}(\rho\frac{\partial}{\partial\rho})+\frac{1}{\rho^2}\frac{\partial^2}{\partial\phi^2}+k_\rho^2) \begin{bmatrix} E_z\\ H_z \end{bmatrix} =0$$

其中$k_\rho^2=w^2\mu\epsilon-k_z^2$

令$\xi=k_p\rho$

我们知道以下方程的解为Bessel Function$J_m(\xi)$和Neumann function$N_m(\xi)$和他们的线性组合

$$[\frac{1}{\xi}\frac{d}{d\xi}(\xi\frac{d}{d\xi})+(1-\frac{m^2}{\xi^2})]B(\xi)=0$$

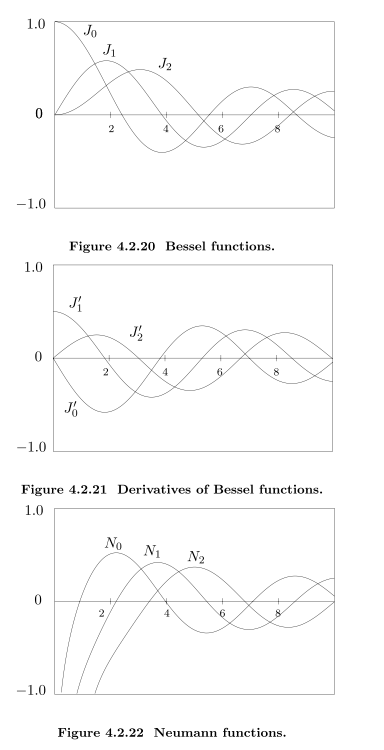
其中

$$J_m(\xi) \to cos(\xi)$$ $$N_m(\xi) \to sin(\xi)$$ $$H_m^{(1)}=J_m(\xi)+iN_m(\xi) \to e^{i\xi}$$ $$H_m^{(2)}=J_m(\xi)-iN_m(\xi) \to e^{-i\xi}$$

往水里扔石头的时候，水波向远处传播的时候，波浪为Bessel函数，在无穷远时接近cos

Circular Metallic Waveguides

TM

$$H_z=0$$ $$E_z=J_m(k_\rho\rho) \begin{bmatrix} sinm\phi\\ cosm\phi \end{bmatrix} e^{ik_zz}$$

色散关系

$$k_z^2+k_\rho^2=w^2\mu\epsilon$$

水平方向电磁场

$$E_\rho=\frac{ik_zk_\rho}{w^2\mu\epsilon-k_z^2}J_m^{'}(k_\rho\rho) \begin{bmatrix} sinm\phi\\ cosm\phi \end{bmatrix} e^{ik_zz}$$ $$E_\phi=\frac{ik_z}{w^2\mu\epsilon-k_z^2}\frac{m}{\rho}J_m(k_\rho\rho) \begin{bmatrix} cosm\phi\\ -sinm\phi \end{bmatrix} e^{ik_zz}$$ $$H_\rho=\frac{-iw\epsilon}{w^2\mu\epsilon-k_z^2}\frac{m}{\rho}J_m(k_\rho\rho) \begin{bmatrix} cosm\phi\\ -sinm\phi \end{bmatrix} e^{ik_zz}$$ $$H_\phi=\frac{iw\epsilon k_\rho}{w^2\mu\epsilon-k_z^2}J_m^{'}(k_\rho\rho) \begin{bmatrix} sinm\phi\\ cosm\phi \end{bmatrix} e^{ik_zz}$$

导波条件

$$J_m(k_\rho a)=0$$ $$\to k_z=\sqrt{w^2\mu\epsilon-(\xi_{mn}/a)^2}$$ $$\to k_{cmn}=\xi_{mn}/a$$

TE

$$E_z=0$$ $$H_z=J_m(k_\rho\rho) \begin{bmatrix} sinm\phi\\ cosm\phi \end{bmatrix} e^{ik_zz}$$

色散关系

$$k_z^2+k_\rho^2=w^2\mu\epsilon$$

水平方向电磁场

$$H_\rho=\frac{ik_zk_\rho}{w^2\mu\epsilon-k_z^2}J_m^{'}(k_\rho\rho) \begin{bmatrix} sinm\phi\\ cosm\phi \end{bmatrix} e^{ik_zz}$$ $$H_\phi=\frac{ik_z}{w^2\mu\epsilon-k_z^2}\frac{m}{\rho}J_m(k_\rho\rho) \begin{bmatrix} cosm\phi\\ -sinm\phi \end{bmatrix} e^{ik_zz}$$ $$E_\rho=\frac{-iw\epsilon}{w^2\mu\epsilon-k_z^2}\frac{m}{\rho}J_m(k_\rho\rho) \begin{bmatrix} cosm\phi\\ -sinm\phi \end{bmatrix} e^{ik_zz}$$ $$E_\phi=\frac{iw\epsilon k_\rho}{w^2\mu\epsilon-k_z^2}J_m^{'}(k_\rho\rho) \begin{bmatrix} sinm\phi\\ cosm\phi \end{bmatrix} e^{ik_zz}$$

导波条件

$$J_m^{'}(k_\rho a)=0$$ $$\to k_z=\sqrt{w^2\mu\epsilon-(\xi_{mn}^{'}/a)^2}$$ $$\to k_{cmn}=\xi_{mn}^{'}/a$$

Resonance谐振腔

波导条件

$$k_xa=m\pi$$ $$k_yb=n\pi$$ $$k_zd=p\pi$$ $$(\frac{m}{a\pi})^2+(\frac{n}{b\pi})^2+(\frac{m}{p\pi})^2=k_r^2$$

其中m,n,p为整数，所以只有特定的频率可以传播

比如，当m=n=1,p=0,$TM_{110}$

$$E_z=E_0sin\frac{\pi x}{a}sin\frac{\pi y}{b}$$ $$H_x=\frac{-i\pi}{w\mu b}E_0sin\frac{\pi x}{a}cos\frac{\pi y}{b}$$ $$H_y=\frac{i\pi}{w\mu a}E_0cos\frac{\pi x}{a}sin\frac{\pi y}{b}$$ $$k_r=\sqrt{(m/2a)^2+(n/2b)^2+(p/2d)^2}K_o$$

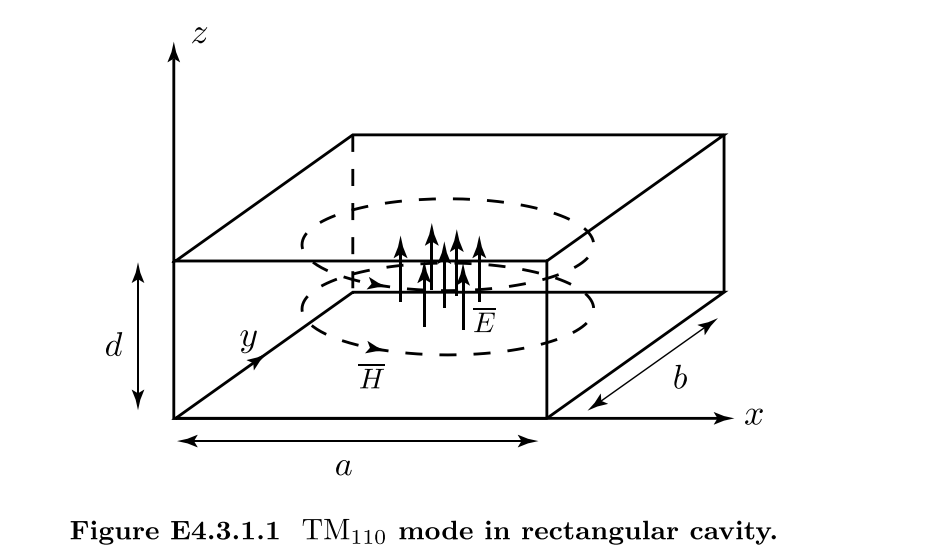
当谐振腔材料不是完全的PEC材料时，在谐振腔内存在损耗和泄露，能量会存在衰减的现象

设总能量函数为U(t)

$$u(t)=U(0)e^{-2\alpha_rt}$$ $$P_d=-\frac{dU}{dt}=2\alpha_rU$$

质量因素

$$Q=w_r/2\alpha_r=w_rU/P_d=w_0L/R$$ $$w_r=k_r/\sqrt{\mu\epsilon}$$