离散时间LTI系统

离散信号单位脉冲分解

对于任意离散信号x[n]，都可以利用移位脉冲的加权之和来表示

$x[n]=\sum_{k=-\infty}^{\infty}x[k]\delta[n-k]$

离散时间LTI系统的卷积和

h[n]为系统对单位脉冲信号的响应

$x[n]=\sum_{k=-\infty}^{\infty}x[k]\delta[n-k]$ $y[n]=\sum_{k=-\infty}^{\infty}x[k]h[n-k]=x[n]*h[n]$

卷积计算方法

公式
列表法：适合小量数据
画图

卷积的性质

交换
结合
分配

x[n] 不为0的区间长度为m，h[n] 为 n，卷积后区间为m+n-1

x[n] 区间为 [m,n], h[n] 区间为 [q,p]
卷积后区间为 [m+q,n+p]

特殊函数的卷积

$x[n]*\delta[n]=x[n]$ $x[n]*\delta[n-n_0]=x[n-n_0]$ $x[n]*u[n]=\sum_{k=-\infty}^{\infty}x[k]u[n-k]=\sum_{k=-\infty}^{n}x[k]$

连续时间LTI系统的卷积积分

任何连续信号也可以分解为脉冲信号，我们可以由此得到连续系统的卷积积分

$\int_{-\infty}^{\infty}x(\tau)h(t-\tau)d\tau=x(t)*h(t)$

连续卷积的积分计算通常要分段积分

连续卷积的性质

交换结合分配与离散情况相同

卷积微分

$\frac{d}{dt}[x(t)*h(t)]$ $=\frac{dx(t)}{dt}*h(t)$ $=\frac{dh(t)}{dt}*x(t)$

卷积积分 $\int_{-\infty}^t[x(\lambda)*h(\lambda)]d\lambda$ $=x(\lambda)*\int_{-\infty}^th(\lambda)d\lambda$ $=h(\lambda)*\int_{-\infty}^tx(\lambda)d\lambda$

积分与微分性质推广

$r^{(i)}(t)=x_1^{(j)}*x_2^{(i-j)}(t)$

其中i, j, i-j取正数时为导数的阶次，负数时为重积分的次数

离散域的差分和累加性质与之类似

与冲激阶跃函数卷积

$x(t)*\delta(t)=x(t)$ $x(t)*\delta(t-t_0)=x(t-t_0)$ $x(t)*\delta'(t)=x'(t)$ $x(t)*u(t)=\int_{-\infty}^{t}x(\tau)d\tau$

LTI系统性质

可逆性

如果一个LTI系统是可逆，那么它就有一个LTI的逆系
统存在，原系统和其逆系统的级联为一恒等系统

稳定性

LTI系统稳定性充要条件为：

$\int_{-\infty}^{\infty}|h(t)|dt<\infty$ $\sum_{n=-\infty}^{\infty}|h[n]|<\infty$

因果性

LTI系统因果性的充要条件

$h[n]=0,n<0$ $h(t)=0,t<0$

LTI系统单位阶跃响应

连续 $s(t)=u(t)*h(t)=\int_{-\infty}^t=h(\tau)d\tau$
离散 $s[n]=u[n]*h[n]=\sum_{k=-\infty}^nh[k]$
与单位冲激响应关系 $h(t)=\frac{ds(t)}{dt}$ $h[n]=s[n]-s[n-1]$

LTI系统的特征函数

复指数信号的重要性在于它是LTI系统的特征函数，利用这样的性质和线性性质，将输入信号分解为指数信号的线性组合就可以化简

$y(t)=e^{st}*h(t)=e^{st}\int_{-\infty}^{\infty}h(\tau)e^{-s\tau}d\tau=H(s)e^{st}$ $y[n]=z^n\sum_{k=-\infty}^{\infty}h[k]z^{-k}=H(z)z^n$

差分方程和微分方程

任意LTI系统的响应都可以利用微分和差分方程表示，比如LC电路

$\sum_{k=0}^na_k\frac{d^k}{dt^k}y(t)=\sum_{k=0}^mb_k\frac{d^k}{dt^k}x(t)$

微分方程解法

微分方程的完全解由两部分组成

$y(t)=y_h(t)+y_p(t)$

求齐次解
- 转化为特征方程
- 求特征根
- 确定齐次解样式
求特解
根据起始条件确定参数

特征根对应函数形式

特征根$\lambda_i$	函数样式
单实根	$C_ie^{\lambda_i(t)}$
k重实根	$(C1t^{k-1}+C_2t^{k-2}……C{k-1}t+C_k)e^{\lambda_i(t)}$
共轭复根$\alpha\pm j\beta$	$e^{\alpha t}(C_1\cos\beta t+C_2\sin\beta t)$
k重共轭复根	$(C1t^{k-1}+C_2t^{k-2}……C{k-1}t+C_k)e^{\alpha t}(C_1\cos\beta t+C_2\sin\beta t)$

常见激励函数对应特解

函数	特解
常数C	常数
$t^m$	$B1t^m……+B_mt+B{m+1}$特征根不等于0。$t^r(B1t^m……+B_mt+B{m+1})$，有r重等于0的实根
$e^{at}$	$Be^{at}$,a不等于特征根。 $B1t^re^{at}……+B_rte^{at}+B{r+1}e^{at}$,a=r重特征根
$\cos\beta t,\sin\beta t$	$B_1\cos\beta t+B_2\sin\beta t$
$t^me^{at}\cos t$	$(B1t^m……+B_mt+B{m+1})e^{at}\cos t+(D1t^m……+D_mt+D{m+1})e^{at}\sin t$

带奇异函数的微分方程——冲激函数匹配法

例子

$i''+4i'+3i=\delta'+3u$ $求齐次解：\lambda=-3,-1$ $i=(C_1e^{-3t}+C_2e^{-t})u(t)$ $求特解，冲激函数匹配\delta '系数相同\to i=u(t)$ $全解：i=(C_1e^{-3t}+C_2e^{-t}+1)u(t)$ $i'=(C_1e^{-3t}+C_2e^{-t}+1)\delta(t)+(-3C_1e^{-3t}-C_2e^{-t})u(t)$ $i''=(9C_1e^{-3t}+C_2e^{-t})u(t)+(-6C_1e^{-3t}-2C_2e^{-t})\delta(t)+(C_1e^{-3t}+C_2e^{-t}+1)\delta'(t)$ $代入方程 \begin{cases} -2C_1+2C_2+4=0\\ C_1+C_2+1=1 \end{cases}$ $\to \begin{cases} C_1=1\\ C_2=-1 \end{cases}$ $\to i=(e^{-3t}-e^{-t}+1)u(t)$

LTI系统响应分解

零输入响应 ：不考虑外加信号, 即输入信号等于零
（x(t)=0 ）, 仅由系统的起始状态（y(0)_ ）所产生的响应。
x(t),t<0部分的响应

零状态响应 ：不考虑系统的起始状态的作用, 即起始状态等于零（y(0)_ ） , 仅由系统的外加激励信号x(t)所产的响应。
x(t),t>0部分的响应

LTI系统响应的求解方法

直接法

根据定义求解两个微分方程再组合

单位冲激函数法

求解单位冲激响应
通过卷积求解两部分响应
利用线性性质进行组合计算

LTI框图

连续
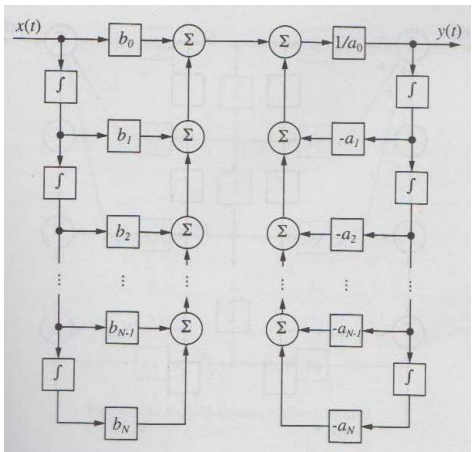
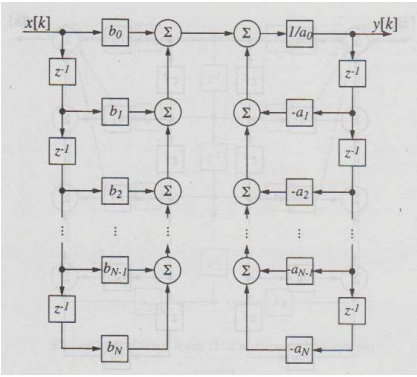
离散