连续时间周期信号的傅里叶级数

复指数信号是LTI系统的特征函数，对于连续时间周期信号，都可以表示为成谐波关系的复指数信号

$x(t)=\sum_ka_ke^{jkw_0t}=\sum_ka_ke^{jk\frac{2\pi}{T_0}t}$ $a_k=\frac{1}{T_0}\int_{T_0}x(t)e^{-jkw_0t}dt$

三角形式的傅里叶级数

$x(t)=B_0+\sum_{k=1}^{\infty}(B_k\cos kw_0t+C_k\sin kw_0t)$ $B_0=\frac{1}{T_0}\int_{T_0}x(t)dt$ $B_k=\frac{2}{T_0}\int_{T_0}x(t)\cos kw_0tdt$ $C_k=\frac{2}{T_0}\int_{T_0}x(t)\sin kw_0tdt$

常见信号的傅里叶级数

三角信号

$x(t)=\sin w_0t=\frac{1}{2j}(e^{jw_0t}-e^{-jw_0t})$

周期方波

$x(t)= \begin{cases} 1&|t|<T_1\\ 0&T_1<|t|<T/2 \end{cases}$ $a_k=\frac{w_0T_1}{\pi}Sa(wT_1)|_{w=kw_0}$

周期方波信号傅里叶级数按1/k衰减

冲激串信号

$\delta_T(t)=\sum_{n=-\infty}^\infty\delta(t-nT)$ $a_k=\frac{1}{T}$

连续时间周期信号傅里叶级数的收敛性

等效性

傅里叶级数是有限项级数近似x(t)的最佳表示

$e_N=x(t)-\sum_{k=-N}^Na_ke^{jkw_0t}$ $E_N=\int_T|e_N(t)|^2dt$ $\lim_{N\to\infty}E_N=0$

收敛性

一个周期信号具有傅里叶级数的表示形式，必需具备条件：
傅里叶系数是一个有限值

收敛条件

$\int_T|x(t)|^2dt<\infty$

狄里赫利（Dirichlet）收敛条件

在一周期内，必须绝对可积

$\int_T|x(t)|dt<\infty$

在一周期间隔内，的最大值和最小值的数目有
限；即在任何有限间隔内，具有有限个起伏变化。
在的一个周期内，只有有限个不连续点，而且在这些不连续点上，函数值是有限的。

吉布斯现象

当用傅里叶级数的前N次谐波分量去近似原来的信号时
会产生 吉布斯(Gibbs) 现象。

信号的间断点两侧将呈现高频起伏和9%超量。
当N增大时，这些高频起伏和超量所拥有的能量将
减少，并趋向于信号的间断点，无论N多大，都不会
消失。但$\lim_{N\to\infty}E_N=0$
均方误差等于零的意义下，傅里叶级数收敛于原
来信号。

连续时间傅里叶变换

对于非周期的信号我们改如何处理？

任意的非周期信号我们可以看做周期为无穷大的周期信号，因此引入了傅里叶变换

比如对于周期方波

$a_k=\frac{w_0T_1}{\pi}Sa(wT_1)|_{w=kw_0}$

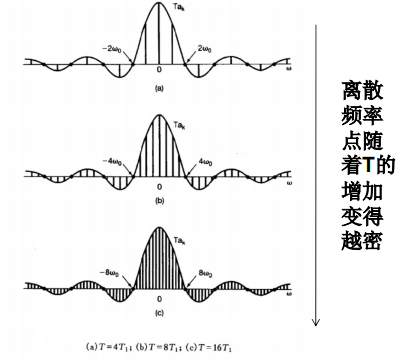
傅里叶变换公式

$X(jw)=\int_{-\infty}^{\infty}x(t)e^{-jwt}dt$ $x(t)=\frac{1}{2\pi}\int_{-\infty}^{\infty}X(jw)e^{jwt}dw$ $x(t)\to X(jw)$

极坐标形式

$X(iw)=|X(jw)|e^{j\theta(jw)}$

连续时间傅里叶变换的收敛条件

$\int_{-\infty}^\infty|x(t)|^2dt<\infty$ $\int_{-\infty}^\infty|x(t)|dt<\infty$

常见函数傅里叶变换

单边指数

$x(t)=e^{-at}u(t),t>0$ $X(jw)=\frac{1}{a+jw}$ $|X(jw)|=1/\sqrt{a^2+w^2}$ $\phi(w)=-arctan(w/a)$

$\frac{t^{n-1}}{(n-1)!}e^{-at}u(t)\to \frac{1}{(a+jw)^n}$

双边指数

$x(t)=e^{-a|t|},a>0$ $X(jw)=\frac{2a}{a^2+w^2}$

单位冲激

$\delta(t) \to X(jw)=1$

冲激偶函数

$\delta'(t) \to jw$

矩形窗函数

$x(t)= \begin{cases} 1&|t|<T_1\\ 0&other \end{cases}$ $X(jw)=2T_1Sa(wT_1)$

高斯脉冲

$x(t)=Ee^{-(\frac{t}{\tau})^2}$ $X(jw)=\sqrt{\pi}E\tau e^{-(\frac{w\tau}{2})^2}$

周期信号的傅里叶变换

周期函数的周期信号会聚集在谐波频率上，在频域上呈冲激函数

$e^{jw_0t} \to 2\pi\delta(w-w_0)$

所以对于周期信号

$x(t)=\sum_{k=-\infty}^{\infty}a_ke^{jkw_0t} \to X(jw)=\sum_{k=-\infty}^{\infty}a_k\delta(w-kw_0)$

连续时间傅里叶变换的性质

线性性质

时移性质

$x(t-t_0)\to e^{-jwt_0}X(jw)$

幅度不变
相位线性变化 $\phi'=\phi-wt_0$
频移性质
$X(j(w-w_0))\to x(t)e^{jw_0t}$
共轭
$x^*(t)\to X^*(-jw)$
x(t)为实值函数，X(jw)实部是偶函数，虚部是奇函数，幅度是偶函数，相位是奇函数
x(t)为实值偶函数，则X(jw)也是实值偶函数
x(t)为实值奇函数，则X(jw)也是纯虚奇函数

微分积分

$\frac{dx(t)}{dt}\to jwX(jw)$ $\int_{-\infty}^tx(\tau)d\tau\to \frac{1}{jw}+\pi X(0)\delta(w)$

尺度变换

$x(at) \to\frac{1}{|a|}X(j\frac{w}{a})$

对偶性

$x(t)\to X(jw)$ $X(t)\to 2\pi x(-w)$

帕斯瓦尔定理

$\int_{-\infty}^\infty|x(t)|^2dt=\frac{1}{2\pi}\int_{-\infty}^\infty|X(w)|^2dw$

周期信号

$\frac{1}{T_0}\int_{T_0}|x(t)|^2dt=\sum_{k=-\infty}^\infty|a_k|^2$

时域卷积性质

$x(t)*h(t)\to X(jw)H(jw)$

调制性质

$x(t)h(t)\to \frac{1}{2\pi}X(jw)*H(jw)$

LTI系统频域响应

LTI系统的频域响应定义为

$H(jw)=\frac{Y(jw)}{X(jw)}=|H(jw)|e^{j\theta(w)}$

一般说来，LTI系统的频域分析法仅适用于稳定系统。

LTI系统频域求解方法

求H
频域相乘
求反变换

周期信号系统响应

$x(t)=\sum_{k=-\infty}^\infty a_ke^{jkw_0t}$ $y(t)=\sum_{k=-\infty}^\infty a_kH(jkw_0)e^{jkw_0t}$