拉普拉斯变换

作用：不是所有的信号可以进行傅里叶变换，引入衰减因子$e^{-\sigma t}$,使$x(t)e^{-\sigma t}$的傅里叶变换收敛

$F\{x(t)e^{-\sigma t}\}=\int_{-\infty}^{\infty}x(t)e^{-\sigma t}e^{-jwt}dt=\int_{-\infty}^{\infty}x(t)e^{-t(\sigma+jw)}dt$ $X(\sigma+jw)=\int_{-\infty}^{\infty}x(t)e^{-(\sigma+jw)t}dt$

其傅里叶反变换

$x(t)e^{-\sigma t}=\frac{1}{2\pi}\int_{-\infty}^{\infty}X(\sigma+jw)e^{jwt}dt$ $x(t)=\frac{1}{2\pi}\int_{-\infty}^{\infty}X(\sigma+jw)e^{t(\sigma+jw)}dt$

令$s=\sigma+jw$

$X(s)=\int_{-\infty}^{\infty}x(t)e^{-st}dt$ $x(t)=\frac{1}{2\pi j}\int_{\sigma-j\infty}^{\sigma+j\infty}X(s)e^{st}dt$

简写为

$X(s)=L\{x(t)\}$ $x(t)=L^{-1}\{X(s)\}$

当x（t）满足傅里叶变换的条件，x（t）的拉普拉斯变换等价于傅里叶变换

拉普拉斯变换的收敛域

ROC：能让x（t）收敛的s范围

x(t)的时域特性与拉氏变换X(s)的收敛域ROC关系

X (s)的ROC在S平面上由平行于jω轴的带状区域构成。
对有理拉氏变换来说，在ROC内不包含任何极点
如果是时限的，并且绝对可积, 则
ROC是整个S平面
如果是右边信号，
而且如果$Re{s}=\sigma_0$这条线位于
ROC 内，那么$Re{s}>\sigma_0$的
全部s值在ROC内。左边信号相反，双边信号为带状
:如果的拉氏变换是有理的，则ROC的边界由
极点限定，或延伸到无穷远，且在ROC内不包含任何极点
如果的拉氏变换是有理的，若是右边信
号，则其ROC 在s平面上位于最右边极点的右边；若是左
边信号，则其ROC 在s平面上位于最左边极点的左边。

常见信号拉氏变换

阶跃信号 $u(t)\underrightarrow{L}=\frac{1}{s}$
冲激信号 $\delta(t)\underrightarrow{L}=1$
单边指数信号 $x_1(t)=e^{-at}u(t)$ $X_1(s)=\frac{1}{s+a} (Re\{s\}>-a)$ $x_2(t)=-e^{-at}u(-t)$ $X_2(s)=\frac{1}{s+a} (Re\{s\}<-a)$
双边指数信号

$x(t)=e^{-|b|t}$ $X_1(s)=\frac{2b}{s^2-b^2} (Re\{s\}<|b|)$

三角信号 $sinwtu(t)\underrightarrow{L^{-1}}\frac{w}{s^2+w^2}$ $coswtu(t)\underrightarrow{L^{-1}}\frac{s}{s^2+w^2}$
幂函数 $t^nu(t)\underrightarrow{L}=\frac{n!}{s^{n+1}}$
指数三角信号 $e^{-at}sinwtu(t)\underrightarrow{L^{-1}}\frac{w}{(s+a)^2+w^2}$ $e^{-at}coswtu(t)\underrightarrow{L^{-1}}\frac{s+a}{(s+a)^2+w^2}$
双边拉氏变换性质
线性性质
- Roc=R1+R2
时移性质 $x(t-t_0)\underrightarrow{L}e^{-st_0}X(s)$ ROC=R
频移性质 $e^{s_0t}x(t)\underrightarrow{L}X(s-s_0)$ ROC=R+Re{s0}
尺度变换 $x(at)\underrightarrow{L}=\frac{1}{|a|}X(\frac{s}{a})$ ROC=aR
共轭

$x^*(t)\underrightarrow{L}X^*(s^*)$

时域卷积 $x_1(t)*x_2(t)\underrightarrow{L}X_1(s)X_2(s)$
时域微分 $\frac{dx(t)}{dt}\underrightarrow{L}sX(s)$
频域微分 $-tdx(t)\underrightarrow{L}\frac{dX(s)}{ds}$
时域积分 $\int_{-\infty}^{t}x(\tau)d\tau=\frac{1}{s}X(s)$ R+Re{s}
初值定理和终值定理
- 若t<0,x(t)=0并且在t=0时,不包含冲激或高阶奇异函数 $x(0^+)=\underset{s\to\infty}{lim}sX(s)$ $x(\infty)=\underset{s\to0}{lim}sX(s)$

周期信号与抽样信号的拉氏变换

周期信号

$X(s)=X_1(s)\sum_{n=0}^{\infty}e^{-nST}$ $=X_1(s)\frac{e^{sT}}{e^{sT}-1}$ $(Re\{s\}>0)$

x1(t)为第一个周期内时间函数

抽样信号

$x_s(t)=x(t)\delta_T(t)\cdot u(t)$ $=\sum_{n=0}^{\infty}x(nT)\delta(t-nT)$ $\underrightarrow{L}\sum_{n=0}^{\infty}x(nT)(e^{-sT})^n$ $如果令e^{sT}=z$ $L[x_s(t)]=\sum_{n=0}^{\infty}x(nT)z^{-n}$ $变为z变换$

拉氏反变换

长除法法
公式法

单边拉氏变换

时域微分 $\frac{dx(t)}{dt}\underrightarrow{UL}s\hat{X}(s)-x(0)$
时域积分 $\int_{-\infty}^{t}x(\tau)d\tau=\frac{1}{s}\hat{X}(s)+\frac{\int_{-\infty}^{0^-}x(\tau)d\tau}{s}$
卷积积分 $x_1(t)*x_2(t)\underrightarrow{L}\hat{X}_1(s)\hat{X}_2(s)$

系统复频域分析

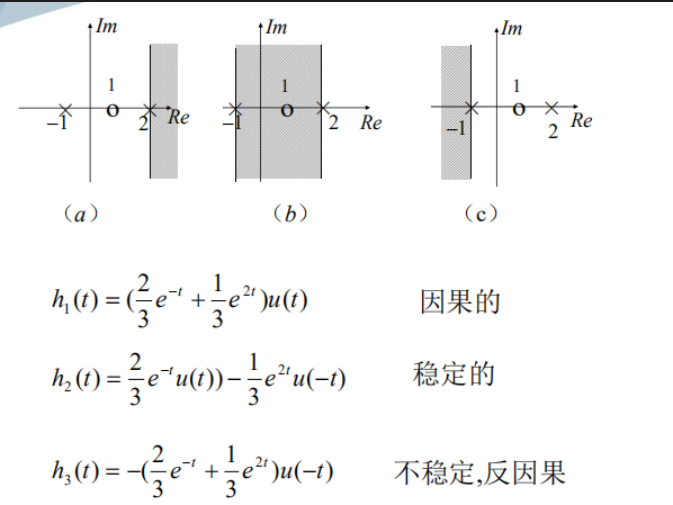
因果性

一个因果LTI系统，其收敛域为右半平面；如果系
统是反因果的，收敛域为左半平面。相反的结论不一
定都成立。

稳定性

稳定系统的冲激响应应是绝对可积，表明稳定系统的频率响应存在。
稳定系统的ROC必包含虚轴（jw轴）

因果稳定系统

$H(s)=\frac{s-1}{(s+1)(s-2)}$

系统响应求解

已知某因果的 LTI 系统的微分方程：$y^{‘’}+3y^{‘}+2y=x(t),y(0^-)=3,y^{‘}(0^-)=-5$，求当
x(t)=2u(t)时系统的全响应、零输入响应、零状态响应。

$取拉氏变换 s^2Y(s)-sy(0)-y^{'}(0)+3sY(s)-3y(0)+2Y(s)=X(s)$ $\to Y(s)=\frac{X(s)+3(s+3)-5}{s^2+3s+2}$ $\to Y_{zi}(s)=\frac{3(s+3)-5}{s^2+3s+2}=\frac{2}{s+2}+\frac{1}{s+1}$ $\to Y_{zs}(s)=\frac{X(s)}{s^2+3s+2}=\frac{1}{s}-\frac{2}{s+1}+\frac{1}{s+2}$ $\to \begin{cases} 零输入响应：y_{zi}(t)=(e^{-t}+2e^{-2t})u(t)\\ 零状态响应:y_{zs}(t)=(1-2e^{-t}+e^{-2t})u(t)\\ 全响应：y(t)=(1-e^{-t}+3e^{-2t})u(t) \end{cases}$

S域原件模型

$\hat{V}_R(s)=R\hat{I} _R(s)$ $\hat{V}_L(s)=sL\hat{I}_L (s)-Li_L (0^-)$ $\hat{V}_C(s)=\frac{1}{sC}\hat{I}_C (s)+\frac{1}{s}v_C (0^-)$ $\hat{I}_R(s)=\frac{1}{R}\hat{V} _R(s)$ $\hat{I}_L(s)=\frac{1}{sL}\hat{V}_L (s)+\frac{1}{s}i_L (0^-)$ $\hat{I}_C(s)=sC\hat{V}_C (s)-Cv_C (0^-)$