Abstract

这篇提出了第一个深度学习模型，成功地直接从高维输入学习控制策略的强化学习。该模型是一个卷积神经网络，使用Q-learing的变体训练，其输入是原始像素，输出是估计未来奖励的Value函数。该方法在七款街机游戏中取得了不错的效果

Background

学习高维度信息比如视觉和语音是强化学习的一大挑战，这样的强化学习非常依赖于数据（特征工程）的质量，而深度学习方法可以很好地提取高维度特征简单来说深度神经网络可以看做一个可以拟合任何复杂函数的工具，只要网络的深度足够大，但是深度学习需要大量人工标注的数据
，而且深度学习假设所有数据是独立同分布的，而强化学习的数据来自于环境，且随环境进行变化。在这篇文章中，作者用卷积神经网络，从复杂的RL环境中的原始视频数据中学习成功的控制策略。该网络用q-学习算法的一个变体进行训练，通过随机梯度下降来更新权值。

environment

在Atari game中我们考虑一个agent与环境$\epsilon$交互的过程，用一个向量$xt$表示当前屏幕显示的图像的像素值，动作（action）定义为当前玩家可以采取的操作，奖励（reward）定义为游戏得分的改变。因为游戏的当前状态不能只用当前的屏幕图像表示，所以作者采用了图像和动作的时间序列 $s_t = x_1, a_1, x_2, …, a{t−1},x_t$来表示状态State
，总结一下，强化学习中各个核心要素在本任务中的表示如下

State：图像和动作的时间序列
Action：玩家采取的操作
Reward：游戏得分的改变

在传统的强化学习（Q-Learning）中我们通常用Bellman 方程来更新Q值，公式如下

$Q^{*}(s, a)=\mathbb{E}_{s^{\prime} \sim \mathcal{E}}\left[r+\gamma \max _{a^{\prime}} Q^{*}\left(s^{\prime}, a^{\prime}\right) \mid s, a\right]$

但在实践中，这种基本方法是完全不切实际的，因为Q函数是为每个序列单独估计的，而没有通用性，我们可以考虑用一个函数来近似Q函数，$Q(s,a;\theta)\approx Q^*(s,a)$,但在强化学习中采用的近似器通常是非线性的，所以我们用一个非线性的近似器-神经网络来近似，我们称之为Q-network，在这个网络训练过程中，损失函数如下定义

$L_{i}\left(\theta_{i}\right)=\mathbb{E}_{s, a \sim \rho(\cdot)}\left[\left(y_{i}-Q\left(s, a ; \theta_{i}\right)\right)^{2}\right]$

其中target为$yi=Q^{*}(s,a)=\mathbb{E}{s^{\prime}\sim\mathcal{E}}\left[r+\gamma \max_{a^{\prime}}Q^{*}\left(s^{\prime}, a^{\prime}\right) \mid s,a\right]$

梯度如下定义

$\nabla_{\theta_{i}} L_{i}\left(\theta_{i}\right)=\mathbb{E}_{s, a \sim \rho(\cdot) ; s^{\prime} \sim \mathcal{E}}\left[\left(r+\gamma \max _{a^{\prime}} Q\left(s^{\prime}, a^{\prime} ; \theta_{i-1}\right)-Q\left(s, a ; \theta_{i}\right)\right) \nabla_{\theta_{i}} Q\left(s, a ; \theta_{i}\right)\right]$

这篇文章采用了off-policy的策略，model-free的方式进行

Deep Reinforcement Learning

不同于一些在线学习的方式，这篇文章中采用了experience replay技术，简单来说就是将每个时间步的状态和动作反馈（$et=s_t,a_t,r_t,s{t+1}$)存储在一个数据集D中,在每次算法内循环中，会从数据集D中随机抽取数据先进行训练，更新Q值，然后执行$\epsilon-greedy$的策略来探索新状态，因为用完整的的时间序列来表示比较困难，所以在算法中用定长序列来表示状态，状态由$\phi$函数表示，具体的算法过程如下

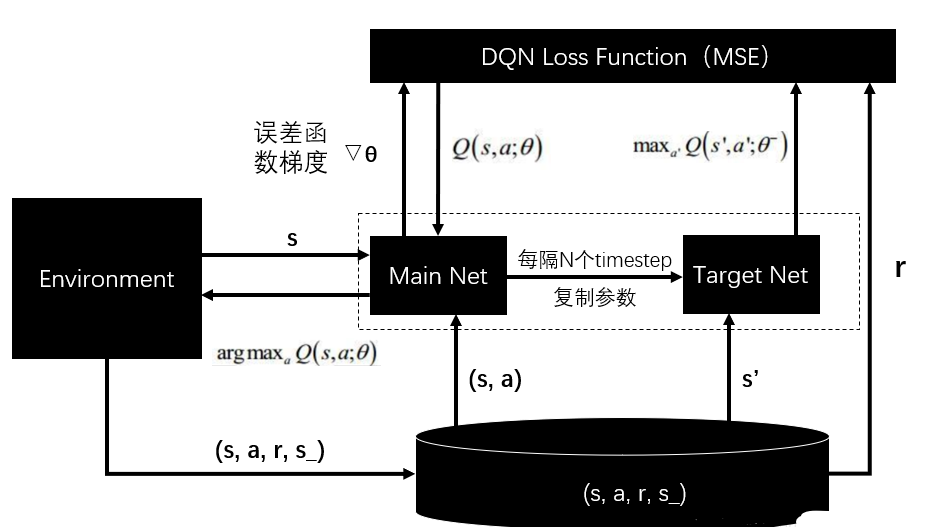
DQN的优点

相比Q-learning，DQN可以在每一步进行多个权重的更新
由于样本之间的强相关性，直接从连续样本中学习效率低效；随机化样本会打破这些相关性，从而减少更新的方差。
当学习策略时，当前参数确定参数训练的下一个数据样本。例如，如果最大化动作是向左移动，那么训练样本将由左侧的样本主导；如果最大化动作然后切换到右边，那么训练分布也会切换。