Radiation
5.2 Green’s Functions格林函数
本章将考虑在有源情况下的麦克斯韦方程,先写出频域有源情况下的麦克斯韦方程
Dyadic Green’s Functions
得到
为了解出这个方程,我们引入格林函数
在数学中,格林函数是一种用来解有初始条件或边界条件的非齐次微分方程的函数。在物理学的多体理论中,格林函数常常指各种关联函数,有时并不符合数学上的定义。
从物理上看,一个数学物理方程是表示一种特定的”场”和产生这种场的”源”之间的关系。例如,热传导方程表示温度场和热源之间的关系,泊松方程表示静电场和电荷分布的关系,等等。这样,当源被分解成很多点源的叠加时,如果能设法知道点源产生的场,利用叠加原理,我们可以求出同样边界条件下任意源的场,这种求解数学物理方程的方法就叫格林函数法。而点源产生的场就叫做格林函数。
其中电流J存在关系
化简得
令
代入化简
当r’=0,即电流不随位置变化
得到
Radiation Field Approximation
当r离辐射源很远时可以进行近似
定义矢量电流矩
得到
5.3Hertzian Dipoles
Hertzian Electric Dipole
最简单的辐射情况是赫兹天线
其电流满足
对应电流矢量矩
电场和磁场
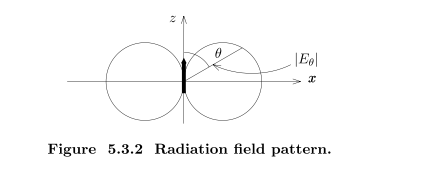
总辐射功率
增益
天线方向被定义为最大增益处,垂直于偶极轴
Linear Dipole Arrays多天线阵列
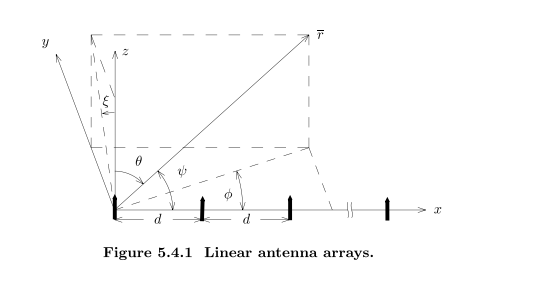
电场和磁场
阵列因子 $\frac{1-e^{inu}}{1-e^{iu}}$
$\alpha$为相邻天线相位差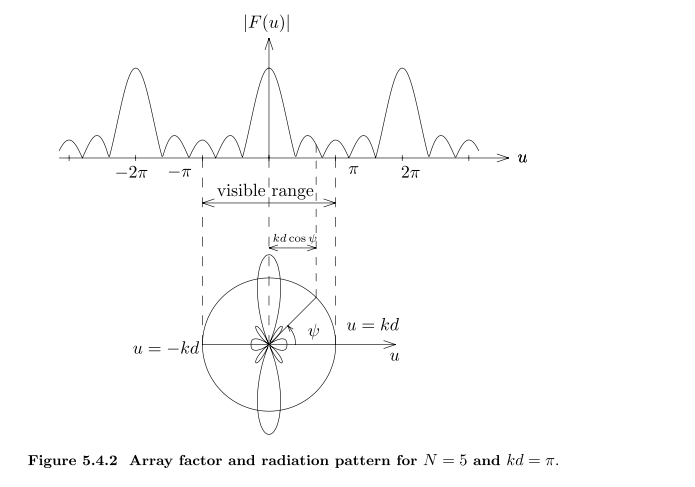
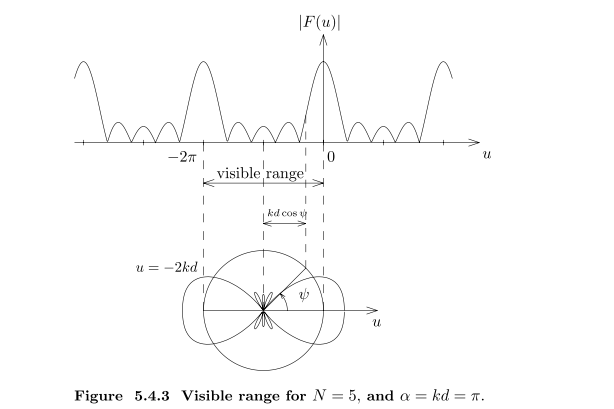
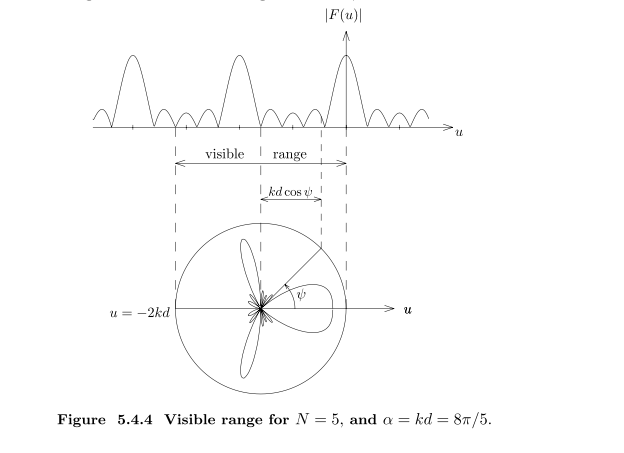
n决定主瓣最大强度,n为天线数量
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 摸黑干活!
评论
