信息熵

信息的基本分类

• 语法信息
• 语义信息
• 语用信息

  符号系统

• X，Y：随机变量
• $x_k,y_j$ 变量取值
• $a_k,b_j$变量取值
• $\chi={x_k;k=1,2…K},\gamma={y_j;j=1,2…,J}$
• 事件：$X=x_k$
• $q_k=Pr{X=x_k}$

事件自信息

我们将特定事件$X=x_k$发生后给外界带来的信息量定义为事件的自信息

$$I(X=x_k)=I(x_k)=-\log q(x_k)$$

a=2的单位为比特

a=e的单位为奈特

事件自信息的本质既是事件对外界提供的信息，也是外界观察心信息付出的代价,通常认为概率越小的事件的信息量越大

条件自信息

$$I(x_k|y_j)=-\log_ap(x_k|y_j)$$

事件Y=yj发生后X=xk发生给外界带来的信息

联合自信息

$$I(x_k,y_j)=-\log_ap(x_k,y_j)$$

X=xk,Y=yj一起发生的信息量

事件互信息

$$I(x_k;y_j)=\log_a\frac{p(x_k|y_j)}{q(x_k)}$$

互信息的本质为事件Y=yj
中包含的有关事件X=xk信息量，即可以是事件X发生的信息量减去事件Y发生后事件X还能给外界提供的信息量

$$I(x_k;y_j)=-\log q(x_k)-[-\log p(x_k|y_j)]$$

互信息的对称性

$$I(x_k;y_j)=I(y_j;x_k)$$

互信息的性质

$$I(x_k;y_j)= \begin{cases} >0 & p(x_k|y_j)>q(x_k)\\ =0 & X,Y独立\\ <0 & p(x_k|y_j)<q(x_k) \end{cases}$$

事件Y中包含X的信息量

条件互信息

$$I(x;y|z)=\log \frac{p(x|y,z)}{p(x|z)}$$ $$=\log \frac{p(x,y|z)}{p(x|z)p(y|z)}$$

联合互信息

$$I(x;y,z)=\log\frac{p(x|y,z)}{p(x)}$$

联合互信息动链式法则

$$I(x;y,z)=I(x;y)+I(x;z|y)$$ $$=I(y;x)+I(z;x|y)$$

变量的平均自信息——熵

$$H(X)=E(I(X))=-\sum_{x\in\chi}q(x)\log_aq(x)$$

• 熵是随机变量不确定性的度量
• 熵是随机变量每次观察结果平均对外界所提供的信息量
• 熵是为了确证随机变量的取值外界平均所需要的与之相
  关的信息量

条件熵

• 以事件 Y=y 为条件的变量X的熵 $$H(X|y)=\sum_{x\in X}p(x|y)I(X|y)=-\sum_{x\in X}p(x|y)\log p(x|y)$$
• 以变量 Y 为条件的变量X的熵 $$H(X|Y)=\sum_{y\in Y}w(y)H(X|y)=-\sum_x\sum_yp(x,y)\log p(x|y)$$

  疑义度，在Y已知X剩余的不确定性

联合熵

$$H(X,Y)=-\sum_x\sum_yp(x,y)\log p(x,y)$$

联合链式法则

$$H(X,Y)=H(X)+H(X|Y)$$ $$=H(Y)+H(Y|X)$$

熵的性质

(5)可加性

$$H(X_2)|_{x_2\in\chi_2}=H(X_1)_{X_1\in\chi_1}+H(X_2|X_1)_{X_2\in\chi_2}^{X_1\in\chi_1}$$

对于变量X可以进行多步观察，每一步都可以从上一步观察的结果中得到更为细致的结果

(6)极值性

$$H_k<\log K$$

均匀分布时熵最大

凸性质

平均互信息

$$I(X;Y)=\sum_x\sum_yp(x,y)\log\frac{p(x|y)}{q(x)}$$

• 非负性
• 对称性
• 互信息与熵的关联性 $$I(X,Y)=H(X)-H(X|Y)=H(Y)-H(Y|X)=H(X)+H(Y)-H(X,Y)$$

  求互信息常用上面的公式,相互独立的事件互信息为0

条件互信息

$$I(X;Y|Z)=\sum_x\sum_y\sum_zp(x,y,z)\log\frac{p(x|y,z)}{p(x)}$$

联合互信息

$$I(X;Y,Z)=\sum_x\sum_y\sum_zp(x,y,z)\log\frac{p(x|y,z}{p(x)}$$ $$=I(X;Z)+I(X;Y|Z)$$

相对熵

一个变量的两种概率分布

$$D(p//q)=\sum_xp(x)\log\frac{p(x)}{q(x)}$$

表示实际分布p(x)和假定分布q(x)之间的平均差距，也称为鉴别熵

相对熵的性质

• 非负 $$D(p//q)>=0$$
• 非对称 $$D(p//q)\not D(q//p)$$
• 与互信息关系 $$I(X;Y)=D(p(xy//p(x)p(y))>=0$$

疑义度

错误概率

$$P_E=\sum_{k=0}^{K-1}\sum_{j\not k}Pr\{X=k,\hat{X}=j\}$$

fano不等式

$$H(X|\hat{X})<=H(P_E)+P_E\log(K-1)$$

马尔可夫链

每个随机变量都是前一个随机变量一步处理的结果,任意一个节点已知，后面的变量和前面没得变量条件独立。

$$p(xyz)=p(x)p(y|x)p(z|y)$$ $$p(z|xy)=p(z|y)$$ $$p(xz|y)=p(x|y)p(z|y)$$ $$Z\to Y\to X$$ $$I(X;Z|Y)=0$$

• 马尔可夫链是可逆的

数据处理定理

如果$X\to Y \to Z$

则$I(X;Y)>=I(X;Z),I(X;Y)>=I(X;Y|Z)$

四变量马尔科夫链

$$graph LR U-->X$$ $$X-->Y$$ $$Y-->V$$ $$I(X;Y)>=I(U;V)$$

互信息的凸性

$$I(X;Y)=I(\{q(x)\},\{p(y|x)\}$$

互信息I(X;Y)是关于输入分布{q(x)}和转移概率矩阵{p(y|x)}的函数

连续随机变量的互信息

$$I(X;Y)=\int\int p_{XY}(x,y)\log \frac{p_{XY}(x,y)}{p_X(x)p_{Y}(y)}dxdy$$ $$I(X;Y|Z)=\int\int\int p_{XYZ}(x,y,z)\log \frac{p(x,y|z)}{p(x|z)p(y|z)}dxdydz$$ $$I(X;YZ)=\int\int\int p_{XYZ}(x,y,z)\log \frac{p(x,y,z)}{p(x)p(yz)}dxdydz$$

基本性质

$$I(X;Y)>=0$$ $$I(X;Y)=I(Y;X)$$ $$I(X;YZ)=I(X;Y)+I(X;Z|Y)$$

连续随机变量微分熵

连续随机变量的熵无穷大，所以引入微分熵的概念来衡量连续变量的相对不确定性

$$H_C(X)=h(x)=-\int p_X(x)\log p_X(x)dx$$

HC (X )不具有线性变换不变性,可正、可负

条件微分熵

$$H_C(X|Y)=-\int\int p_{XY}(x,y)\log p(x|y)dxdy$$

联合微分熵

$$H_C(X,Y)=-\int\int p_{XY}(x,y)\log p(x,y)dxdy$$ $$=H_C(X)+H_C(Y|X)$$ $$=H_C(Y)+H_C(X|Y)$$

微分熵极大化

峰值受限

若 峰值受限于[-M,+M] 即 则 X为均匀分布微分熵最大

$$H_C(X)<=In 2M$$

功率受限

若X的方差不大于$\sigma^2$,则X为高斯分布时微分熵最大

$$H_C(X)<=1/2In 2\pi e\sigma^2$$

熵功率

• 定义连续随机变量 的熵功率为 $$\hat{\sigma_X^2}=\frac{1}{2\pi e}e^{2H_C(X)}$$
• 高斯随机变量的微分熵 $$H_C(X)=\frac{1}{2}In(2\pi e\sigma^2)$$
• 高斯变量熵功率 $$\hat{\sigma_X^2}=\frac{1}{2\pi e}e^{2H_C(X)}=\sigma^2$$

熵功率不等式

$$H_C(X)<=In(2\pi e\sigma^2)$$ $$\hat{\sigma_X^2}=\frac{1}{2\pi e}e^{2H_C(X)}<=\sigma^2$$

功率一定时，高斯变量的熵功率最大，与功率相等

平稳源

平稳源：任意长度的片段的联合概率分布与时间起点无关

$$Pr(X_1X_2...X_N=x_1x_2...x_N)=Pr(X_{L+1}X_{L+2}...X_{L+N}=x_1x_2...x_N)$$

简单无记忆源

$$Pr(X_1X_2...X_N=x_1x_2...x_N)=\prod_{n=1}^N Pr(X_n=x_n)$$

平稳源的熵

平均每符号熵

$$H_N(X)=\frac{1}{N}H(X_1X_2...X_N)$$

熵速率

$$H_{\infty}(X)=\lim_{N\to \infty}H_N(X)$$

熵相对率

$$\eta=\frac{H_{\infty}(X)}{\log K}$$

信源冗余度

$$R=1 -\eta$$

平均条件熵

$$H(X_N|X_{N-1}X_{N-2}...X_1)$$

平稳源熵的性质

• 单调增
• $HN(X)>=H(X_N|X{N-1}…X_1)$
• $H{\infty}(X)=\lim{N\to\infty}HN(X)=\lim{N\to\infty}H(XN|X{N-1}…X_1)$

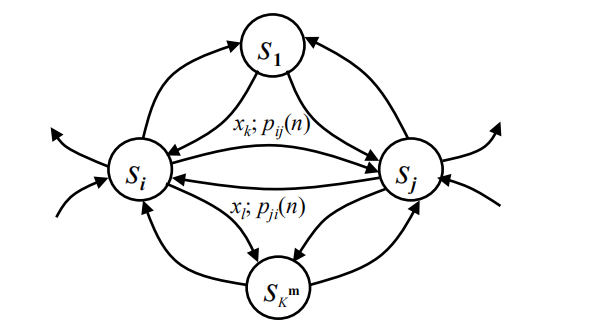
马尔科夫源

$$Pr(X_l|X_{l-1}X_{l-2}...X_1X_0)=Pr(X_{l}|X_{l-1}...X_{l-m})$$

马尔科夫源的状态图

• 时齐（时不变）马尔科夫源：状态转移概率pij(n)与时间n无关。
  到达任一其它状态。
• 既约（不可约）马尔科夫源：
  从任一状态出发，经有限步总可以
• 状态转移概率矩阵： $$P=[p_{ij}]_{K^m\times K^m}$$
• n时刻的状态概率分布： $$Q(n)=(q_1(n),q_2(n)...q_{K^m}(n))$$ $$Q(n+1)=Q(n)P$$
• 对时齐既约马尔科夫源，状态的稳态分布存在 $$\hat{Q}=\lim_{n\to \infty}Q(N+1)=\lim_{n\to \infty}Q(n)P=\hat{Q}P$$

  马尔科夫的熵率

  $$H_{\infty}=H(X|S)$$