信息编码
信息获取的本质
离散无记忆信源DMS的编码
目标:在代价最小的意义上来有效表达一个信源,包括量化,压缩,映射,变化,自然语言翻译等许多抽象的过程
DMS编解码系统概念框图
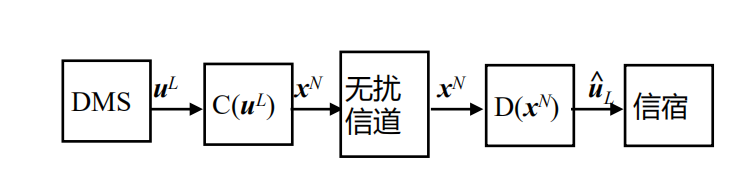
绝对无差错编码
DMS
- 编码符号集
- 对于源U的任意L长序列用编码符号集$\Beta$进行绝对无差错等长编码,则必有编码速率
平均每个信源符号编码所需时间
- 信源熵
AEP性质(渐进等分)
离散无记忆信源U输出一个L长的序列
因为无记忆性,所以
- 序列的信息为
- 每个符号平均自信息为期望方差性质由切比雪夫不等式给定$\epsilon$,当L充分大时所以这表明当L充分大的时候$\frac{1}{L}I(u^L)\to H(U)$
这一性质被称为渐进等分性质
典型列集合
为给定DMS输出长度为L的$\epsilon$ 典型列集合,简称典型列集,其中$u^L\in U^L$。
典型列集合可以理解为序列的自信息接近信源熵的序列
典型列集合性质
- 当L足够大时
- 典型列性质2
- 典型列性质3
DMS编码定理
对熵为H(U)的离散无记忆信源所输出的L长序列进行等长编码,编码序列长为N,编码符号表包括 D个可用编码符号.则当平均每信源符号所耗用的编码比特数(编码速率)$R=\frac{N\log D}{L}$满足
可实现渐进无差错的编码
不等长码
平均码长定义
| 信源消息 | 出现概率 | 码1 | 码2 | 码3 | 码4 |
|---|---|---|---|---|---|
| $a_1$ | 0.5 | 0 | 0 | 0 | 0 |
| $a_2$ | 0.25 | 0 | 1 | 01 | 10 |
| $a_3$ | 0.125 | 1 | 00 | 011 | 110 |
| $a_4$ | 0.125 | 10 | 11 | 0111 | 1110 |
唯一可译性
如果一个码的扩展是非奇异的,则该码唯一可译
所谓编码的后缀分解集就是如下递归构成的一系列集合,${S_i}$
举例
| $S_0$ | $S_1$ | $S_2$ | $S_3$ | $S_4$ | $S_5$ | … | |
|---|---|---|---|---|---|---|---|
| 0 | 2 | 1 | 0 | 1 | 0 | … | |
| 10 | 2 | 2 | 2 | ||||
| 12 | 12 | 12 | |||||
| 21 | 122 | 122 | |||||
| 112 | 1 | ||||||
| 1122 |
编码唯一可译的充要条件是所有的后缀分解集都不包含码字
即时可译性
异字头码
如果一个码没有一个码字是其他码字的前缀,则该码被称为前缀码或者异字头码
我门可以用D元树构造异字头码
Kraft定理
Kraft定理阐明了什么样的码长可以构造一个唯一可译的码
存在长度为$n_1,n_2…n_k$的D元异字头码的充要条件为
如果一个码可译,则Kraft不等式成立,存在一个同样长度的异字头码
不等长编码定理
任何D元唯一可译码满足
证明
任何唯一可译码必然满足Kraft不等式。
当所有码字都在叶节点上取到等号
一定存在一个D元的唯一可译码,使得
编码速率
编码效率
对于DMS
不等长编码定理扩展
对于长度为L的平稳遍历源$U^L$
有
若源离散无记忆,进一步有结论
最佳不等长编码(Huffman编码)
那么我们如何可以得到一个平均码长最短的编码?
最佳不等长码:在给定信源分布的情况下,在平均码长最短的意义上最佳
我们从最简单的二元最佳码看起
其符合性质
- 出现概率越小的码越长
- 出现概率最小的两个消息对应码长相等,且其码字只有最后一位不同
我们把消息出现的概率降序排列,码字长度升序排列
为什么出现概率最小的两个消息码长相等且只有一位相反?
因为没有一个码是另一个码的前缀
辅助源
对于辅助源的最佳编码也是
将辅助源的概率最小的两个编码在结尾分别加上0和1
可递归编码定理
对辅助源U’对最佳编码也是对原始源的最佳编码
Huffman编码案例

D元Huffman编码虚拟消息的合并
- 若$K=(D-1)i+1$,则每次均有D个消息要合并,短标号得到充分利用
- 若$K=(D-1)i+M$,则每次必须增补D-M个概率为0的虚拟消息,使得最后一次合并仍然有D个消息,从而充分利用短标号
‘
Huffman编码的排序问题
在消息数量巨大的时候,对信息排序是不可能的,需要一些其他的算法
Shannon编码
对于给定信源
用长度为
的编码将$P_k$二进制展开([x]表示大于x的最小整数),截取前$l_k$作为编码
第k个消息的自信息
香农yyds!!!
- 唯一可译
- 异字头
- 融合自信息
Shannon编码的异字头性
香农编码的效率
和哈夫曼编码比,香农编码渐进收敛性差,但竞争性更好
Fano编码
对
U进行概率对分
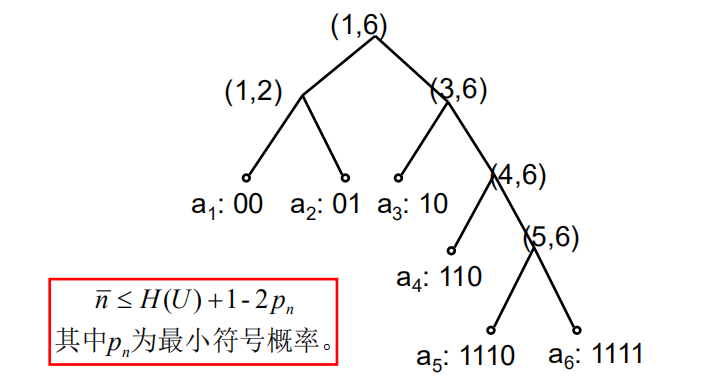
fano编码本质上是一个二叉决策树
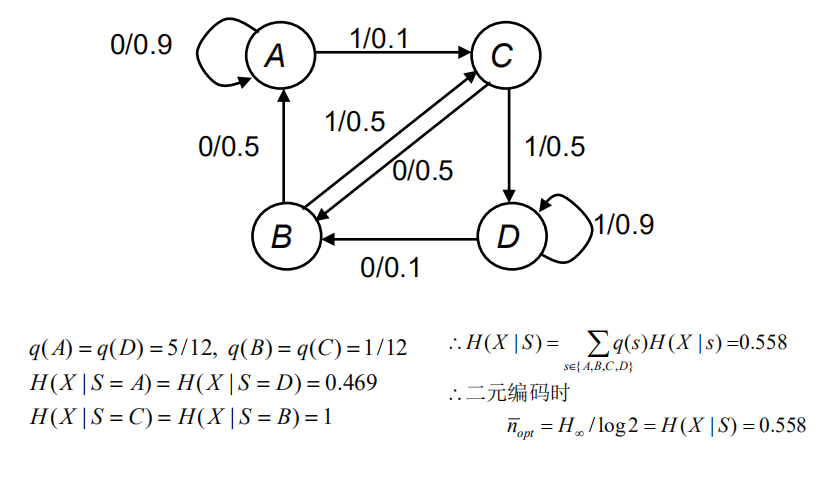
其中$p_n$为最小符号概率。
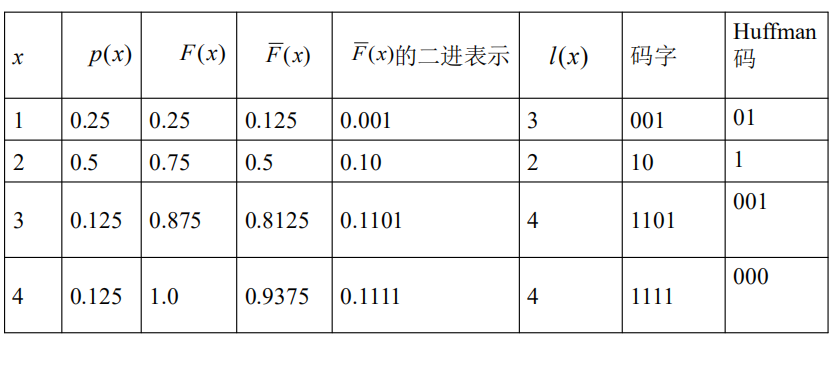
Shannon-Fano-Elias编码
优点:不需要排序
记
为累计概率分布
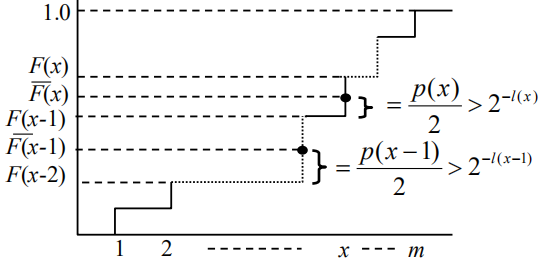
SFE编码效率
算术编码
sequential encoding的思想
- 基本思想
- SFE编码的直接推广(从单个符号到n长序列)
- 关键点
- 累计概率快速有效迭代算法
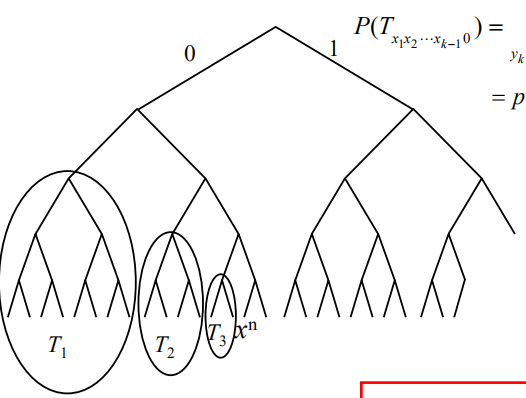
定义
是指
$x^n$对应的子区间
算术编码的基本算法
算数编码的关键思想在于建立了一套计算信源出现概率$p(x^n)$和累计概率$F(x^n)$的算法
比如,设二元消息$$
这样的好处是当序列长度从n变到n+1时,容易计算概率
通用信源编码
针对未知概率分布的信息
香农编码在不能准确获得信源分布的事性能恶化
Z-L编码
序列的分解
在每个前面未出现的最短序列编号
1|0|11|01|010|00|10|…
平稳信源编码
令$\epsilon$是任意小正数,对平稳有记忆信源${U^L,p(u^L)}$进行不等长D元编码,则总可以找到一个$L(\epsilon)$,当$L>L(\epsilon)$平均编码码长 $\bar n$满足
马尔可夫源