通讯的本质是准确或者近似地恢复在另一个点所选择的信息的过程

信道和其分类

物理信道：噪声信道，干扰信道，衰落信道，存储信道
按输入/输出信号在幅度和时间上取值的连续性
- 幅度离散，时间离散信道
- 幅度连续，时间离散信道
- 幅度离散，时间连续信道
- 幅度连续，时间连续信道
按输入/输出的记忆性
- 有记忆信道
- 无记忆信道
输入/输出信号的关系确定性
- 确定信道
- 随机信道

信道抽象模型

离散无记忆信道 $p_N(y^N/x^N)=\prod_{n=1}^Np(y_n|x_n),\forall N$
平稳信道 $p(y=_n|x_n=k)=p(y_m|x_m),\forall n,m$ 记为 $\{\chi;p(y|x);Y\}$
互信息容量
$\lim_{n\to \infty}\frac{1}{n}\max_{\{Q(x^n)\}}I(X_1X_2...X_n;Y_1Y_2...Y_n)$

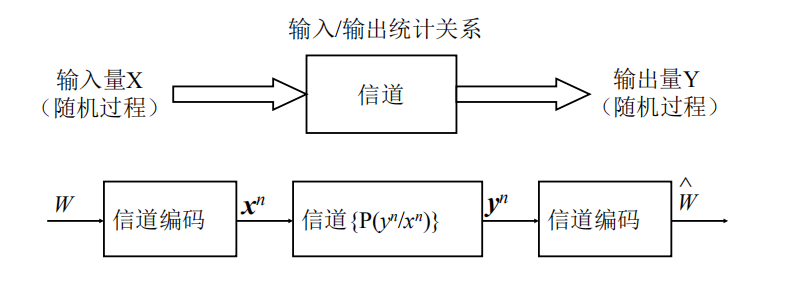
信道容量定义为每次利用信道，在输入和输出符号之间所能提供的互信息的最大值的极限

离散无记忆信道容量

$I(X_1X_2...X_n;Y_1Y_2...Y_n)<=\sum_{i=1}^nI(X_i;Y_i)$

等号在输入为独立随机序列时达到

$I(X_1X_2...X_n;Y_1Y_2...Y_n)<=\sum_{i=1}^nI(X_i;Y_i)=nI(X;Y)$

从而

$C=\max_{\{Q_k\}}I(X;Y)$

${Q_k}$为X的概率分布

无噪信道

由于信道是无噪的,从接收到的Y可完全确定X,所以

$H(X|Y)=0$

从而

$I(X;Y)=H(X)$

当输人入分布为等概分布时H(X)达到最大,即

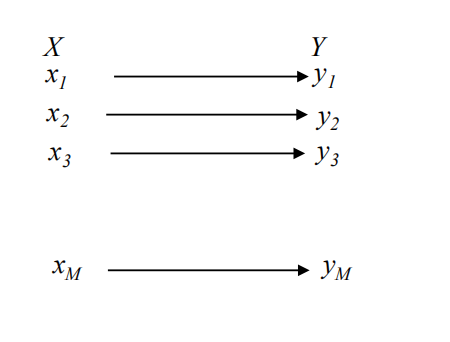
$C=\max_{\{Q_k\}}I(X;Y) \\ =\max_{\{Q_k\}}H(X) \\ \sum_{i=1}^M-\frac{1}{M}\log \frac{1}{M} \\ =\log M$

无损信道

$C=\log M$

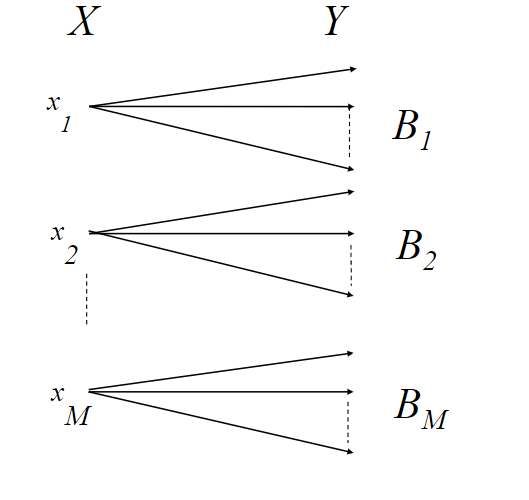
确定信道

我们不知道发射端端信息，但知道落在那个集合，存在一定的疑义度

$C=\log m$

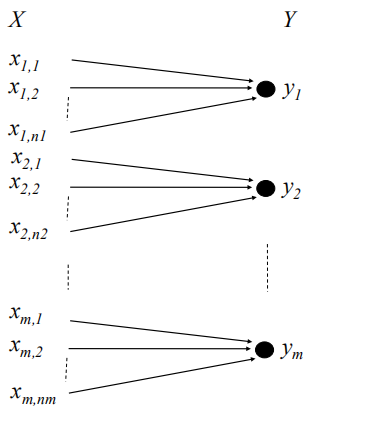
无用信道

无用信道的特征是对任何输人分布,I(X;Y)=0,也就是说信道容量C为零。等效地要求对任何输入分布H(X|Y) = H(X),也等价地要求随机变量X和Y彼此独立,所以

$C=0$

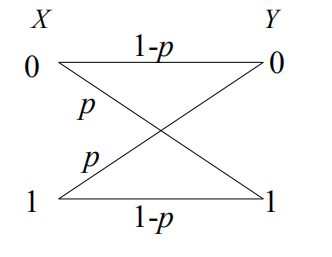
二进制对称信道（BSC）

$I(X;Y)<=1-H(p)$

输入等概率取等号

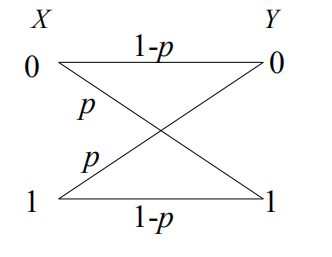
$H(p)$为二元分布的熵

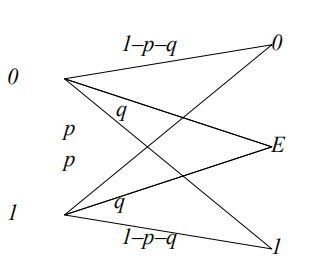
二进制删除信道（BEC）

$C=\max_{\{Q_k\}} H(Y)-H(p) \\ H(Y)=H(p)+(1-p)H(q) \\ C=\max_q(1-p)H(q) \\ =1-p$

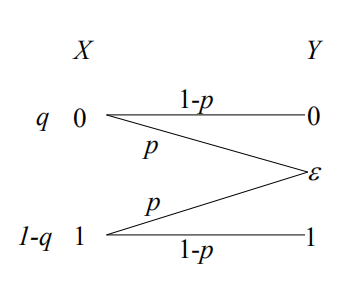
当输入为等概率分布时，等号成立

BEC和BSC比较

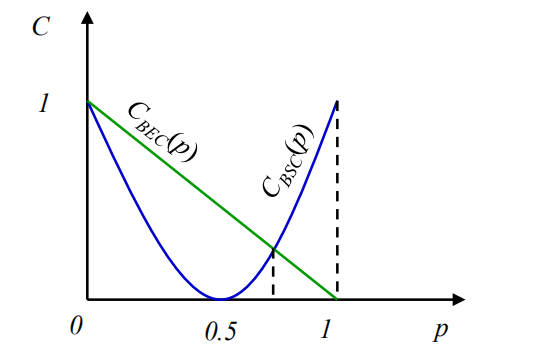
离散无记忆信道容量定理

信道容量问题可以看做约束优化问题

$C=\max_{\{Q_k\}}I(X;Y) \\ s.t. \\ \begin{cases} Q_k>=0&k=0,1,2...,K-1\\ \sum_kQ_k=1 \end{cases}$

概率分布${Q0,Q_1…Q{K-1}}$达到转移概率为${p(j|k)}$的离散无记忆信道容量C的充要条件为:

$\begin{array}{l} I(X=k;Y)=C &\forall k,Q_k>0\\ I(X=k;Y)<=C &\forall k,Q_k=0 \end{array}$

其中$I(X =k;Y)$表示通过信道传送字符X =k时,信道的输入与输出之间可获得的互信息的期望值，即

$I(X=k;Y)\sum_{j=0}^Jp(j|k)\log\frac{p(j|k)}{\sum_{i=0}^{K-1}Q_ip(j|i)}$

证明

采用拉格朗日乘子法

$J\{Q_k\}=I(X;Y)-\lambda(\sum_{k=0}^{K-1}Q_k-1) \\ \frac{\partial J\{Q_k\}}{\partial Q_k} \\ =I(X=k;Y)-(1+\lambda)$ $I(X=k;Y)= \begin{cases} 1+\lambda&\forall Q_k>0\\ <1+\lambda& \forall Q_k=0 \end{cases}$

令
$C=1+\lambda$

$I(X=k;Y)=\sum_{k=1}^{K+1}Q_kI(X=k;Y)=1+\lambda=C$

对称离散无记忆信道

$P=\{p(j|k)\}=\begin{bmatrix} p(0|0)&p(1|0)&...&p(J-1|0)\\ p(0|1)&p(1|1)&...&p(J-1|1)\\ ...&...&...&...\\ p(0|K-1)&p(1|K-1)&...&p(J-1|K-1) \end{bmatrix}$

若P中每一行都是第一行的一个
置换，则该信道关于输入对称。

$H(Y|X)=H(Y|X=k) \\ =-\sum_{j=0}^{J_1}p(j|k)\log p(j|k)$

若P中每一列都是第一列的一个
置换，则该信道关于输出对称

$\sum_{k=0}^{K_1}p(j|k)=\frac{K}{J} \\ j=0,1,...J-1$

若一个信道既关于输入对称，又关于输出对称，即P中每一行都是第
一行的一个置换，每一列都是第一列的一个置换，则该信道是对称的

对一个信道的转移概率矩阵P按列划分，得到若干子信道，若划分出
的所有子信道均是对称的，则称该信道是准对称的

达到准对称离散无记忆信道容量的输入分布为均匀分布。

若信道关于输入对称

$I(X;Y)=H(Y)+\sum_{j=0}^{J-1}p(j|k)\log p(j|k)$

若信道同时也关于输出对称（即信道对称）
$C=\log J+\sum_{j=0}^{J-1}p(j|k)\log p(j|k)$
若信道只关于输入对称
$C<=\log J+\sum_{j=0}^{J-1}p(j|k)\log p(j|k)$

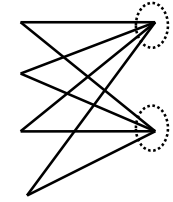
k元对称信道

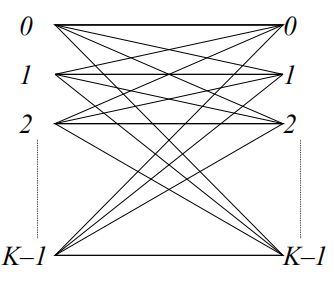
$p(j|k)=\begin{cases} 1-p&k=j\\ \frac{p}{K-1}&k\not = j \end{cases}$

$C=\log K-H(p)-p\log(K-1)$

二进制删除信道

$P=\begin{bmatrix} 1-p-q&q&p\\ p&q&1-p-q \end{bmatrix}$

$C = I(X = 0;Y ) = I(X = 1;Y ) \\ =(1-p-q)\log(1-p-q)+p\log p-(1-q)\log\frac{(1-q)}{2}$

模k加法信道

$Y=X+ZmodK$ $X,Y,Z \in \{0,1,2...K-1\}$

p(z)为任意分布

此时的转移概率为p(z)

$H(Y|X)=H(z)$

所以

$C=\log K-H(z)$

转移概率矩阵可逆信道容量计算

当转移概率矩阵P可逆，信道容量可以估计

假定输入字符概率$Q_k>0, k =0,1,…,K -1$,是达到信道容量的分布

$I(X=k;Y)=\sum_j p(j|k)\log\frac{p(j|k)}{\sum_iQ_ip(j|i)}=C, k=0,1...K-1$

令$wj=\sum{i=0}^{K-1}Q_ip(j|k)$

$\sum_{j=0}^{K-1}p(j|k) \log p(j|k)-\sum_{j=0}^{K-1}\log w_j=C \to \sum_{j=0}^{K-1}[C+\log w_j]=\sum_{j=0}^{K-1}p(j|k) \log p(j|k)$

令

$\beta_j=C\log w_j \\ \to w_j=2^{\beta_j-C}$

由约束条件$\sum w_j=1$

可以解出

$C=\log\sum_j 2^{\beta_j}$

进一步由$wj=\sum{i=0}^{K-1}Q_ip(j|k)$求出${Q_k
}$

信道组合

平行信道
开关信道

index modulation

级联信道

平行信道

我们一般假设两个信道完全独立无关

等号在信道分别独立用最佳分布发送时成立

$C=C_1+C_2$

开关信道

$p(j|k)=\begin{cases} p_1(j|k)&\\ p_2(j|k)&\\ 0&other \end{cases}$ $Q_k=\begin{cases} P_AQ_k^1&\\ P_BQ_k^2&\\ \end{cases}$ $I(X;Y)=P_AI(X_1;Y_1)+P_BI(X_2;Y_2)+H(P_A;P_B)$ $C=\max_{\{P_A,Q_k^1,Q_k^2\}}I(X;Y)$ $C=\log[2^{C_1}+2^{C_2}]$

其中

$P_A=2^{C_1-C} \\ P_B=2^{C_2-C}$

级联信道

$I(X;Y)>=I(X:Y) \\ I(Y;Z)>=I(X;Y) \\ C<=\min\{C_1,C_2\}$

离散无记忆信道编码

编码速率 $R=\frac{\log M}{n}\to C$

基本定义

离散无记信道(X,p(y/x),Y)上的一个(M,n)码由如下组成:

一个与M个消息相对应的标号集合{1,2,… ,M }:
一个编码函数$X^n(.):{1,2,……,M}\to X^n$，所得到的码
字为$X^n(1),X^n(2),…X^n(M)$;一个码的全体码字构成码书。
译码函数$g(.):Y^n\to {1,2,M}$，对应于确定的译码
法则，帮助接收者根据接收到序列Y”来确定发送消息是什么。
错误概率
发送第i个消息所发生的错误概率 $\lambda_i=P\{g(Y^n)=\not i|X^n=X^n(i)\}$
（M，n）码的最大错误概率定义为 $\lambda^{(n)}=\max \lambda_i$
（M，n）码的平均错误概率定义为 $P_e^{(n)}=\frac{1}{M}\sum_{i=1}^M \lambda_i$

速率可达性:
若存在一系列$(2^{nR}，n）$码，当$n\to \infty$时，最大错误概率$\lambda^{(n)}$，则R被称为可达的。

联合典型列

相对于联合分布p(x,y)的联合典型列集合$A_{\epsilon}^{(n)}$
是指具有下述性质的序列对$(x^n,y^n)$的集合

$A_{\epsilon}^{(n)}=\{(x^n,y^n)\in x^n\times Y^n \\ |-\frac{1}{n}\log p(x^n)-H(X)|<\epsilon \\ |-\frac{1}{n}\log p(y^n)-H(Y)|<\epsilon \\ \{|-\frac{1}{n}\log p(x^n,y^n)-H(XY)|<\epsilon\}$

联合典型列性质

若联合序列$(X^n,Y^n)$的每一个符号对$(x_i,y_i)$均是按照联合分布p(x,y)独立选取，即$(X^n,y^n)\to p(x^n,y^n)$,则

$Pr((X^n,Y^n)\in A_{\epsilon}^{(n)})\to 1$
$(1-\epsilon)2^{n(H(XY)-\epsilon)}\leq |A_{\epsilon}^{(n)}|\leq 2^{n(H(XY)+\epsilon)}$
如果联合序列$(\hat{X}^n,\hat{Y}^n)\to p(x^n,y^n)$,即$\hat{X}^n$和$\hat{Y}^n$分别按照p(x,y)的边缘分布p(x)和p(y)来独立选取，则

$(1-\epsilon)2^{-n(I(X;Y)+3\epsilon)}\leq Pr((\hat{X}^n,\hat{Y}^n)\in A_{\epsilon}^{(n)})\leq 2^{-n(I(X;Y)-3\epsilon)}$ $M\approx \frac{2^{nH(Y)}}{}$

离散无记忆信道编码

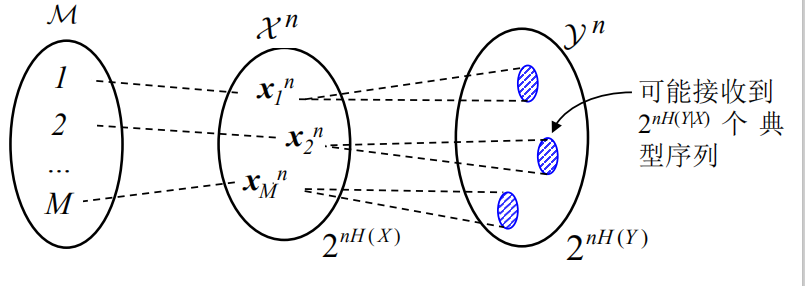
随机选择$y^n$,约有$^{2-nI(X;Y)}$的概率与$x^n$构成联合典型

$M\approx \frac{2^{nH(Y)}}{2^{nH(Y/X)}}= 2^{nH(Y)-nH(Y|X)}=2^{nI(X;Y)}\\ R=\frac{\log M}{n}\approx I(X;Y)\to C$

信道编码定理

所有低于信道容量C的速率R均是可达的,即当R<C时，总存在一系列码$(2^{nR}, n)$,当$n \to \infty$时，最大误码概率元 $\lambda^{(n)}\to 0$。

离散无记忆信道编码定理

渐进无差错准则
- 所谓可靠通信是指随着码长增大，错误概率可以任意小，但并非为零;
- 信道上不是仅传输一个符号，而是传输一串很长符号序列。由于多次使用信道，从而可以利用大数定律获得随机编码的统计性能
随机编码
- 计算在一类随机选择的码书上的平均错误概率。因此至少存在一个码
  书（即一个编码），它的错误概率和在码书集合上计算的平均错误概
  率一样好
联合典型译码
- 采用联合典型的准则进行译码，并且这样的译码准则是统计最优的 $P(E)=\sum_{B}P(B)P_e^(n)(B)=\sum_BP(B)\frac{1}{M}\sum_{w=1}^M\lambda_w(B) \\ =\frac{1}{M}\sum_{w=1}^M\sum_BP(B)\lambda_w(B)=\sum_BP(B)\lambda_1(B)$

离散无记忆信道编码逆定理

具有$λ^{(n)} \to 0$的任何$(2^{nR},n)$码必有 $R \leq C$

信源和信道分离编码与联合编码

信源/信道分离编码 $if H<R_s<R_c<C \to P_e\to 0$
信源、信道联合编码
- 在有限集上取值的信源V的熵速率为H(V).
- 若H(V) < C,则存在一个信源信道联合编码，使得$P_e^{(n)} \to 0$;
- 反之,若H(V) > C,则不可能以任意小的错误概率传送信源。

只要H<C,总可以找到可行的信源信道联合编码；也可以分别构造最优的信源编码和信道编码，使信息传输可达；
信源信道联合编码不能使得可行速率极限增加，但可以简化编码

时间离散的加性高斯信道

$Y_i=X_i+Z_i \\ \frac{1}{n}\sum_{i=1}^nx_i^2\leq P$

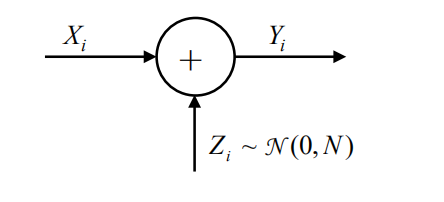
高斯信道容量

$Y_i=X_i+Z_i \\ X_i\in \{+\sqrt{P},-\sqrt{P}\}$

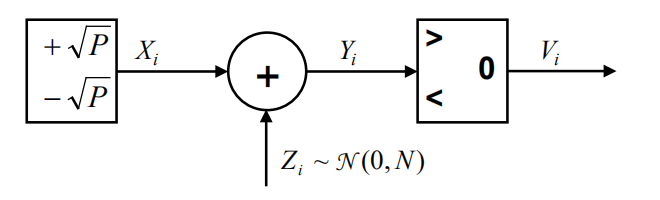
加性高斯信道的容量

$C=\max_{p(x):EX^2\leq P}I(X;Y)$ $I(X;Y)=h(Y)-h(Y|X) \\ =h(Y)-h(X+Z|X) \\ =h(Y)-h(Z|X) \\ =h(Y)-h(Z)$ $h(Z)=\frac{1}{2}\log 2\pi eN \\ EY^2=E[(X+Z)^2]=P+N \\ h(Y)<=\frac{1}{2}\log 2\pi e(P+N)$

香农公式

$I(X;Y)<=\frac{1}{2} \log 2\pi e(P+N)-\frac{1}{2}\log 2\pi eN \\ =\frac{1}{2}\log (1+P/N)$

当输入X为高斯分布时等号成立

高斯信道编码定理

在噪声方差为N,信号功率受限为P的加性高斯信道上，任何R<C的速率均是可达的，其中

$C=\frac{1}{2}\log (1+P/N)$

在高斯信道上任何R >C的速率均是不可达的

高斯平行信道

$C=\frac{1}{2}\sum_{i=1}^k\log(1+\frac{(v-N_i)^+}{N_i})$

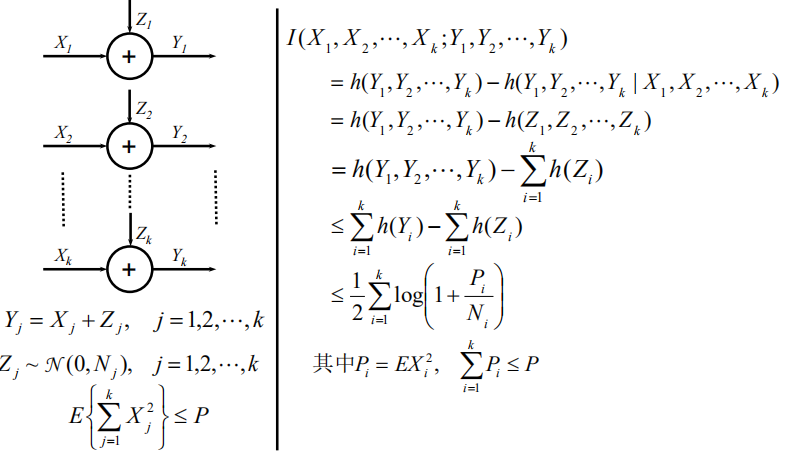
注水法则

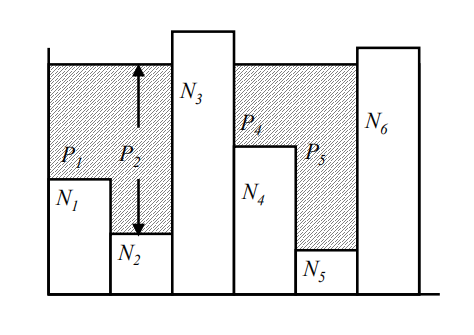
模拟高斯信道容量

$y(t)=x(t)+z(t)$

x(t),z(t)的带宽均限制在[0,W ]Hz之内。连续信号的离散化表示（Shannon抽样/Nyquist抽样）

$f(t)=\sum_{n=-\infty}^{\infty}f(\frac{n}{2W})\sin 2\pi W(t-\frac{n}{2W})$

考虑T秒钟的模拟传输过程，它相当于2WT次平行的传输。设每次传输时输入样本X,的方差分别为P,,则由功率限制

$\sum_{i=1}^{2WT} P_i \leq PT$

T秒钟的传输容量：

$C_T=\frac{1}{2}\sum_{i=1}^{2WT}\log (1+\frac{P_i}{N_i}) \\ N_i=\frac{N_0}{2} \\ P_i=(v-\frac{N_0}{2})^+=\frac{P}{2W} \\ C_T=WT \log\{1+\frac{P}{N_0W }\}$

等效地，每秒钟的容量

$C=W\log \{1+\frac{P}{N_0W}\}bit/s$

Shannon带限信道容量定理的重要启示

$W\to \infty,C\to \frac{P}{N_0}\log e(bps)$

频率利用率 $\eta =\frac{R}{W}$
比特传输能量 $E_b=\frac{P}{R}$

通讯的本质是准确或者近似地恢复在另一个点所选择的信息的过程

信道和其分类

信道抽象模型

互信息容量

离散无记忆信道容量

无噪信道

无损信道

确定信道

无用信道

二进制对称信道（BSC）

二进制删除信道（BEC）

BEC和BSC比较

离散无记忆信道容量定理

对称离散无记忆信道

k元对称信道

二进制删除信道

模k加法信道

转移概率矩阵可逆信道容量计算

信道组合

平行信道

开关信道

级联信道

离散无记忆信道编码

基本定义

错误概率

联合典型列

联合典型列性质

离散无记忆信道编码

信道编码定理

离散无记忆信道编码定理

离散无记忆信道编码逆定理

信源和信道分离编码与联合编码

时间离散的加性高斯信道

高斯信道容量

加性高斯信道的容量

高斯信道编码定理

高斯平行信道

注水法则

模拟高斯信道容量

Shannon带限信道容量定理的重要启示