固态电子基础

能带

/	自由电子	孤立原子中的电子	固体中的电子
外力源	无	单一原子核及同一原子的其它电子	众多原子核及其电子
能量分布	连续谱	能级	能带

电子的共有化运动形成能带

KP模型

通过绝热近似把问题转化为单体多电子问题

波函数为以下形式

$$\psi(x)=u(x)e^{jkx}$$

势函数具有空间周期性

$$U(x)=U(x+na)$$

波函数同时也具有周期性

$$\psi(x+na)=e^{jkna}\psi(x)$$

布洛赫定理：电子在一个周期性的势场运动单电子的波函数为一个周期，振幅周期为晶格周期

波函数	自由电子	布洛赫电子	孤立原子中的电子
波函数	Aexp(jkx)平面波	u(x)exp(jkx)布洛赫波	f（r）束缚电子
运动区间	空间各点	晶体中	原子核周围
运动形式	自由运动	共有化运动	束缚运动

在共有化运动的情况下的波函数

本征方程

$$F(E)=f(\alpha a)=P'\frac{\sin(\alpha a)}{\alpha a}+\cos (\alpha a)=\cos(ka)$$

本征方程决定了E和k的关系：色散关系

$$\alpha^2=(2m/\hat{h}^2)E$$

k空间

$$F(E)=f(\alpha a)=P'\frac{\sin(\alpha a)}{\alpha a}+\cos(\alpha a)=\cos(ka)$$

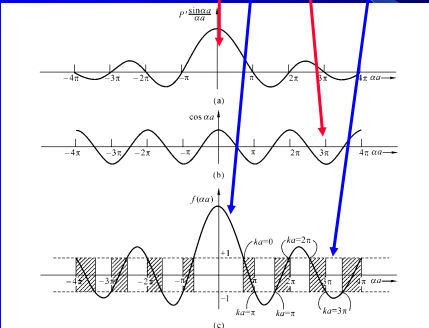
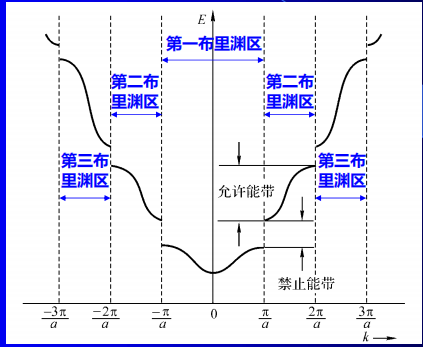
能带理论其他模型

自由电子模型

金属的电子受到束缚很小，以接近自由电子的方式运动，所以用自由电子的薛定谔方程近似

紧束缚模型

• 每个原子对电子有比较强的束缚作用

为什么用E-k的关系，（能带图）来描述电子行为？

• 从波动的角度来看电子
• 波动行为最重要的关系是色散关系（w-k关系）

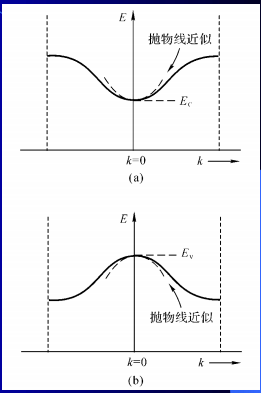
固体电子的导电性，有效质量，空穴

信息物理的最终目标是建立起能带和固体伏安特性之间的关系

电子能带全空或者全满都不导电

电子运动速度

$$v=\frac{dE}{\hbar dk}$$

• 群速度 $$v=\frac{dw}{dk}$$
• 相速度 $$v=\frac{w}{k}$$

  电子加速度

  $$a=\frac{dv}{dt}$$ $$=\nabla_k \frac{dE}{\hbar dt}$$ $$dE=Fr=Fvdt$$ $$\to \frac{dE}{dt}=F\nabla_k\frac{E}{\hbar}$$ $$\to a=\nabla_k^2\frac{1}{\hbar^2}FE(k)$$

电子有效质量

$$F+F_c=m_0a$$ $$F=m^*a$$ $$\to m^*=\frac{F}{F+F_c}$$

有效质量反映了晶格的作用

• $m^*>0$，外力可以让电子加速，但比自由电子慢
• $m^*<0$，晶格势场比外力大的多，并且反向，电子无法加速

• m*不是电子的惯性质量，而是在能量周期场中电子受外力作用
  时，在外力与加速度的关系上相当于牛顿力学中的惯性质量；
• m*不是一个常数，而是k的函数。一般情况下，它是一个张量，
  只有特殊情况下，它才可化为一标量的形式。
• m可以是正值，也可以是负值，特别有意义的是：在能带底附
  近，m总是正值，表示电子从外场得到的动量多于电子交给晶
  格的动量，而在能带顶附近，m*总是负的，表示电子从外场得
  到的动量少于电子交给晶格的动量。

满带，部分填充的能带和空穴

我们从能带的角度来认识导电性

能带全空和全满都不导电，只有半填充才导电

电子能态变化与导电性

• 无外场 $$E\approx\hbar^2k^2/2m$$ $$E(-k)=E(k)$$ $$v=dE/\hbar dk$$ $$v(-k)=-v(k)$$ 所以k与-k的两个电子对电流贡献抵消，晶体总电流为0

• 加入外场
  外场对电子开始做功 $$\frac{dk}{dt}=\frac{F}{\hbar}$$

k空间，电子能态变化速率为

$$v_k=dk/dt=-e|E|/\hbar$$

$v_k$不是速度

• 空穴导电

$$J_1'=J_1+J_e=J_1=\frac{-e}{V}v(k_1)=0$$ $$J_1=ev(k_1)/V$$

金属，绝缘体和半导体

• 各种·晶体都有各自的能带
• 价电子是构成化学键的电子
• 价电子决定化学性质
• 价电子能级分裂形成的能量带为价带

绝缘体

• 导带为空穴，不导电
• 价带为满带，不导电
• 禁带宽度很大，约6eV

金刚石。$E_g=5.6eV$

半导体

• 导带和价带为部分填充，导电
• 禁带宽度比绝缘体小的多，约为1eV

在绝对零度时，半导体也不导电

金属

• 导带为部分填充能带，导电
• 价带为部分填充能带，导电
• 价带为部分填充能带

半金属

• 导带和价带有少许交叠

一维概念带三位扩展

• 不同方向有不同的原子间距，不同的位函数

间接间隙带隙半导体材料适合作微电子材料，不适合光电子器件材料

半导体中的载流子

载流子：载运电流的粒子

• 金属：自由电子
• 半导体：导带电子，价带空穴

如何计算载流子的浓度？

• 计算单位体积中能带中单位能量包含的能级（量子态）数目（态密度函数1）
• 计算每个能级（量子态）被电子占据的概率
• 对整个能带积分从而得到电子的浓度

把材料看作一个高楼，每个楼层有若干个房间（态密度），每个房间的人数（电子占据概率），对整个楼层进行积分

态密度函数

单位体积，单位能量允许电子占据量子态数目

我们用三维无限深势井中的自由电子在近似金属和半导体中的电子

$$\psi(x)=\sqrt{2/a}\sin(kx)$$ $$k=\frac{n\pi}{a}$$ $$k^2=\frac{2mE}{\hbar^2}$$

在三维的情况下类似

$$k^2=2mE/\hbar^2=k_x^2+k_y^2+k_z^2$$ $$k_i=n_i\pi/a$$

在k空间，两个量子态间距为$\pi/a$，考虑泡利不相容原理，，一个自旋量子态体积为$0.5(\pi/a)^3$

态密度公式

$$g_E(E)dE=(4\pi a^3/h^3)(2m)^{3/2}E^{1/2}dE$$

单位体积、单位能量允许电子占据的量子态数目

$$g(E)=4\pi(2m/h^2)^{3/2}E^{1/2}$$ $$=\frac{4\pi(2m)^{3/2}}{h^3}\sqrt{E}$$

对于半导体我们用有效质量来代替实际质量，在导带底部

$$E\approx E_c+dEk/dk+d^2Ek/dk^2$$ $$E\approx E_c=\hbar^2kk^2/2m$$ $$g_c=\frac{4\pi(2m)^{3/2}}{h^3}\sqrt{E-E_c}$$

费米分布函数与费米能级

玻尔兹曼分布

传统气体分子分布

$$f==exp[-E/k_BT],k_B玻尔兹曼常数$$

全同粒子

经典粒子都可以一一区分，量子中的粒子用波函数描述，在波函数重叠时不能一一区分

玻色子——爱因斯坦分布

玻色子

• 自旋为$\hbar$的整数倍（0, $\hbar$ , 2$\hbar$ , 3$\hbar$ , …）
• 粒子不可区分
• 没有泡利不相容原理
• 波函数具有交换对称性
• 多个玻色子可以挤进同一能态
• 光子、π介子等无质量粒子

分布函数

$$f(E)=\frac{g_i}{-1+exp(E-\mu)/k_BT}$$

费米-狄拉克分布

费米子

• 自旋为$\hbar$的半整数倍$(\pm\frac{1}{2}\hbar,\pm\frac{3}{2}\hbar,\pm\frac{5}{2}\hbar…)$
• 质子、电子、中子
• 满足泡利不相容原理 $$f(E)=\frac{g_i}{1+exp(\frac{E-E_F}{k_BT})}$$ $$k_B=1.381\times10^{-23}J/K$$ 不同温度下的费米几率函数
  
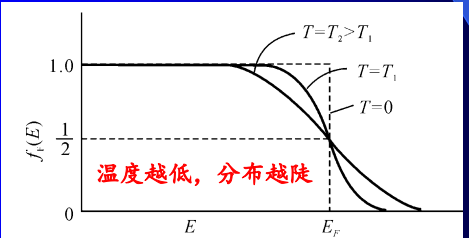
  费米能级EF：描述电子统计分布的物理量，量纲为eV
• T = 0 K：
  • E > EF，f(E) = 0，完全没有电子
  • E < EF，f(E) = 1，完全由电子占据
• T > 0 K：
  • E > EF，f(E) < 1/2
  • E < EF，f(E) > 1/2
  • E = EF，f(E) = 1/2

• 在k空间，自由电子的等能面为球面， $E = E_F$的等能面为
  费米面

• $E_F = k_BT_F，T_F$为费米温度

  $$f_F(E)=\frac{1}{1+exp(\frac{E-E_F}{k_BT})}$$

• 对于本征半导体，$E_F$位于禁带中部

  $$E_F-E_v==E_C-E_F==0.5E_g$$
• Eg ：1.6 ~ 7 eV
• 半导体的费米温度TF ：$10^4 - 10^5 K$
• 室温：$T = 300K，k_B
  T = 4.142*10^{-21}J = 0.0259 eV$
• 价带顶: $exp(*) = e^{-30} - e^{-135}$
  ， f (E) - 1 ，价带主要由电子充满
• 导带底: $exp(*) = e^{30} - e^{135}
  ， f (E) ~ 0$，导带电子很少
• $f_F(E)$和$1 - fF (E)$以$E_F$为对称
• $f_F(E)$为粒子占据能带带几率（导带能级被电子占据的几率）
• $1-f_F(E)$是能态未被电子占据的几（能态空占的几率）
• 对于本征半导体，从导带底部开始计算 $(E– E_F
  )/(k_B
  T ) >> 1$，此时分布可以近似为玻尔兹曼-爱因斯坦分布+.

$$f(E)=exp(-\frac{E-E_F}{k_BT})$$

半导体中的载流子

当T>0K时，电子被热激发，价带电子进入导带，导带电子，价带空穴，使导带，价带都带电

k空间能带结构

• 导带抛物线近似 $$E_C(k)=E_{C0}+\hbar^2k^2/(2m_n^*)$$
• 价带抛物线近似 $$E_V(k)=E_{V0}-\hbar^2k^2/(2m_p^*)$$

  导带电子浓度

  $$n_0=\int_{E_{C0}}^{E_{C1}}f(E)g_n(E)dE$$ $$=N_Cexp(-\frac{E_{C0}-E_{F0}}{k_BT})$$

  导带有效态密度函数

  $$N_C=2(\frac{m_n^*k_BT}{2\pi \hbar^2})^{3/2}$$

价带空穴浓度

$$p_0=N_Vexp(-\frac{E_{F0}-E_{V0}}{k_BT})$$

导带有效态密度函数

$$N_V=2(\frac{m_p^*k_BT}{2\pi \hbar^2})^{3/2}$$

费米能级

$$E_{F0}(T)=E_i+\frac{3}{4}k_BTIn(\frac{m_p^*}{m_n^*})$$

禁带中心

T>0K,费米能级
在禁带中部附近

$$E_i=\frac{1}{2}(E_{V0}+E_{C0})$$

禁带宽度

$$E_g=E_{C0}-E_{V0}$$

本征半导体平衡载流子浓度与温度、禁带宽
度bandgap energy有关，与费米能级无关

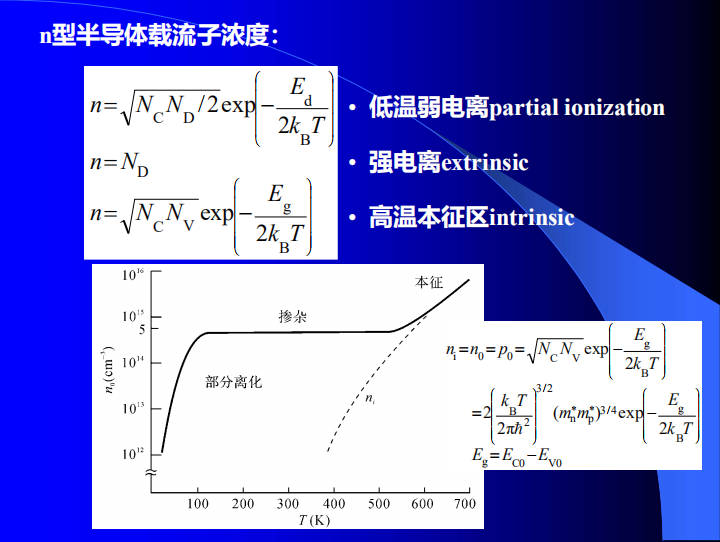
本征半导体载流子

$$n_0=p_0=n_i=\sqrt{N_CN_V}exp(-\frac{E_g}{2k_BT})$$

材料	硅（Si）	砷化镓（GaAs）	锗（Ge）
Nc (cm-3)	$2.8*10^{19}$	$4.7*10^{17}$	$1.04*10^{19}$
Nv (cm-3)	$ 1.04*10^{19}$	$7.0*10^{18}$	$6.0*10^{18}$
$m_n^*/ m0$	1.08	0.067	0.55
$m_p^*/m0$	0.56	0.48	0.37
ni (cm-3)	$1.5*10^{10}$	$1.8*10^6$	$2.4*10^{13}$

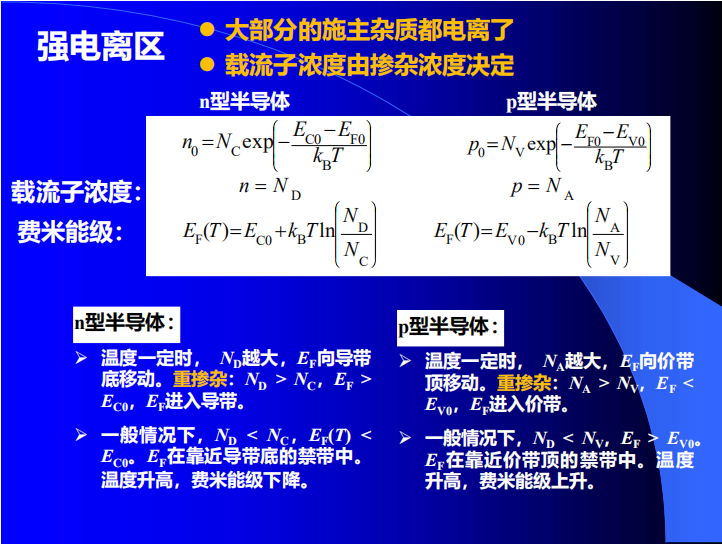
杂质半导体

• 浅能级杂质
  • 浅能级施主/受主杂质的能级离导带底/价带顶很近
  • 浅能级施主原子很容易电离、施主离子很难俘获电子
  • 浅能级受主原子很容易电离、受主离子很难俘获空穴
  • 浅能级杂质的电离能可以用类氢原子模型近似分析
• 深能级杂质
  • 深能级施主/受主杂质的能级离导带底/价带顶都很远
  • 深能级杂质原子很难电离，很难为导带或价带提供载流子
  • 深能级杂质的电离能不可以用类氢原子模型

施主原子密度$N_D$

$$n_d\approx gN_Dexp(-\frac{E_D-E_F}{k_BT})$$

受主原子密度$N_A$

$$p_a\approx gN_Aexp(-\frac{E_F-E_A}{k_BT})$$

补偿半导体compensated semiconductor：

既掺施主杂质，也掺受主杂质

• ND> NA，为n型半导体
• ND< NA，为p型半导体
  
  
  
  
  

  金属中的自由电子

  金属中的电子可以用自由电子气模型代替能带理论
• 单位空间体积中金属的能态密度 $$g(E)=4\pi(2m_0/h^2)^{3/2}E^{1/2}$$
• 电子浓度 $$n=\frac{8\pi}{3}(\frac{2m_0}{h^2})^{3/2}E_F^{3/2}$$
• 费米能级 $$E_F\approx\frac{h^2}{2m_0}(\frac{3n}{8\pi})^{2/3}$$

• E = EF的等能面为费米面

  • 自由电子的费米面：理想时为球面
  • 实际的费米面：与球面有较大区别

• T = 0 K：

  • E > EF，完全没有电子
  • E < EF，完全由电子占据（电子占满能态）

• T > 0 K：

  • EF - kBT < E < EF的电子跃迁到
    EF
    < E < EF+ kBT的能态上

    电阻率和温度

    金属电导率

    金属中电子在外电场下做漂移运动,平均速度与电场强度成正比 $$v_d=\mu E$$ $$J=-nev_d$$ $$\to \sigma=-ne\mu$$ 杂质、缺陷、晶格振动使载流子收到散射

• 散射使载流子恢复无规则热运动

• 平均漂移速度消失

两次散射之间自由时间的平均值，称为弛豫时间τ

实际上，载流子速度不同，因而弛豫时间不同，迁移率也不同。
若考虑载流子速度统计分布的性质，需用统计理论计算τ

在费米面附近的电子对电导有贡献,所以实际电导为

$$\sigma=\frac{ne^2\tau(E_F)}{m_n^*}$$

半导体电阻率

半导体中含有两种载流子

$$\sigma =ne\mu_n+pe\mu_p$$

载流子迁移率和浓度都是温度的函数,温度升高导致晶格振动载流子散射增强

• 迁移率 $$\mu=\mu_L+\mu_I$$ $$\mu \in T^{3/2}$$
• 低温
  温度上升，迁移率由$\mu_I$主导，迁移率上升，电阻率下降
• 中温
  温度上升，迁移率由$\mu_L$主导，迁移率下降，电阻率上升
• 高温
  温度上升，在载流子浓度上升，迁移率下降，电阻率下降

半导体材料

• 半导体材料：
  • 元素半导体：Si、Ge、Se（硒）、Te（碲）……
    +化合物半导体：晶态、非晶态无机、有机化合物、氧化物
• 双元素
• 三元素
• 四元素

非晶态半导体材料

• 非晶Si（α-Si）半导体：太阳电池、场效应管（驱动液晶
  显示，逻辑电路和图像传感器）
• 硫属玻璃半导体：奥氏（Ovshinsky）效应（奥氏阈值开关、
  奥氏记忆开关）
  • 氧化物玻璃半导体：ITO导电玻璃

固态电子效应

• 磁电效应
• 光电效应
• 热电效应
• 压电效应
• 声电效应
• 磁光效应
• 光磁电效应
• 热磁电效应
• 光磁电效应

磁电效应

• 霍尔迁移率 $$J_x==en\mu_HE_x$$ $$\to \mu_H=I_xL/(enV_xWd)$$

• 测定霍耳系数RH(单位电流密度和单位磁感应强度产生的霍尔电场)：

  $$R_H = E_y /(J_xB_z ) = (V_H/W)/[I_xB_z /(Wd)] = (V_Hd)/(I_xB_z)$$

• 确定半导体的导电类型：

  • n型半导体：RH < 0；
  • p型半导体：RH > 0

    耿氏效应

    速度饱和:velocity saturation:

n型GaAs，平均漂移速度vd并非
一直随电场强度上升而上升，有一个饱和值（电场强度3000
V/cm时，达到最大值）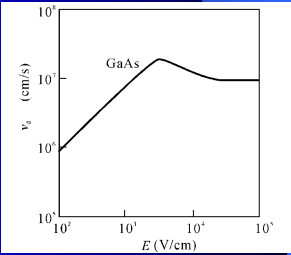

固态电子能谱

我们使用单色光轰击样本，电子受到激发通过分析电子能量分布来获取信息

俄歇电子能谱

$$E_A=E_K-E_{L1}-E_{L2,3}-\phi$$

• $E_A$俄歇电子能量
• $EK-E{L1}-E_{L2,3}$能级电子结合能
• $\phi$样品功函数