半导体器件
PN结特性概述
平衡PN结
- n区
- 施主杂质
- p区
- 受主杂质
因为存在载流子浓度差,空穴从p区向n区扩散,电子从n区向p区扩散,结p区侧聚集负离子(电离受主),结n区侧聚集正离子(电离施主),形成了,负空间电荷区,正空间电荷区,阻止进一步扩散,形成并增强相反方向的漂移运动,扩散与漂移的动态平衡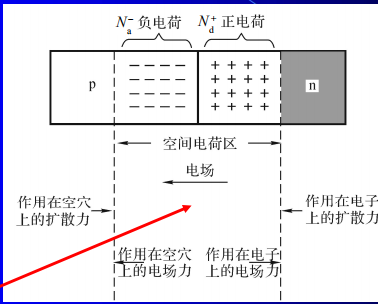
- 同质结:以两种相同的半导体单晶材料为基础
- 异质结:以两种不同的半导体单晶材料为基础
- pn结: 在导电类型相反的半导体单晶材料交界处形成
- 高低结:在导电类型相同的半导体单晶材料交界处形成
n区导带的电子进入p区导带存在$V_D$的势垒,称为内建电势,也称为接触电位差
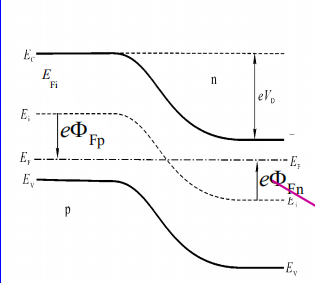
对此,我们有关系
- n区导带电子浓度
- 本征半导体所以
- 完全电离情况下同理对于p区
- 本征半导体所以
- 完全电离情况下
我们可以得到
其中$V_T=\frac{k_BT}{e}$,称为热电压
室温热电压(thermal voltage):
$V_T= 0.026 V$
同质突变pn结
同质突变pn结电荷分布和电场分布
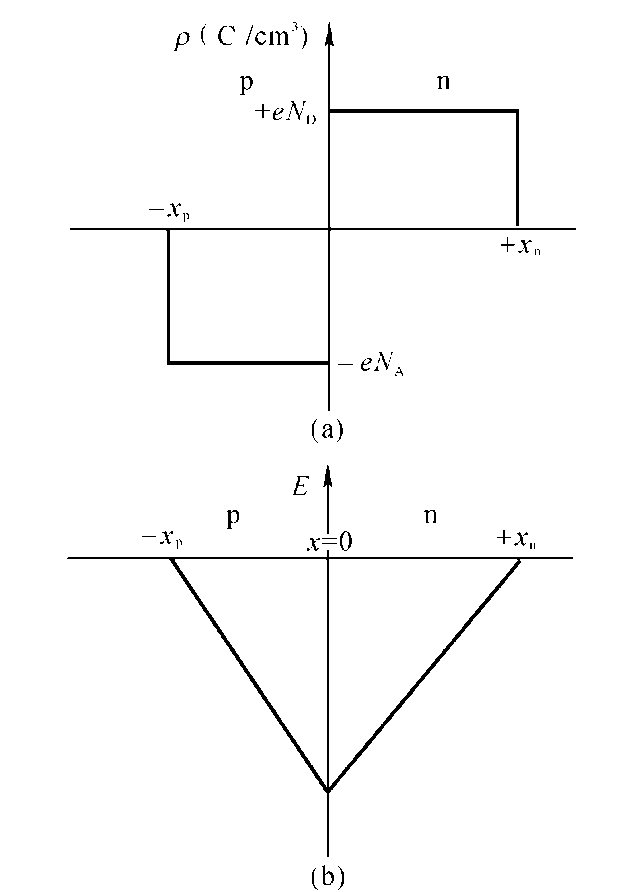
电位分布
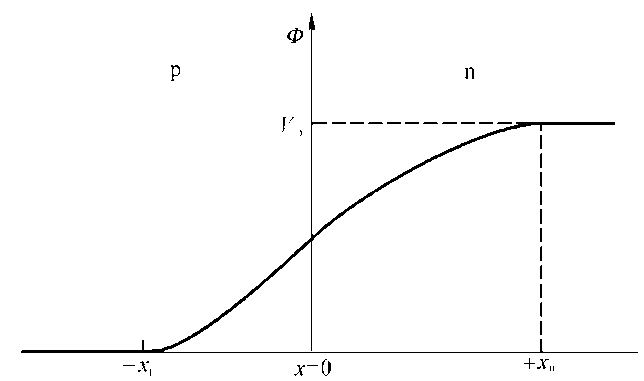
$\epsilon_r$为半导体电容率
空间电荷区宽度space charge width
3.3.5半导体连续性方程
均匀掺杂半导体在热平衡下,单位时间、单位体积
电子空穴对的:产生数 = 复合数
在外界(光或电)作用下,载流子浓度与平衡值有偏离,产生非平衡载流子。n型半导体光照后增加载流子,非平衡少子浓度:$\Delta p$
- 少子扩散
- 扩散diffusion流密度(单位时间、通过单位面积的粒子数):
- 空穴扩散流密度:$S_p$
- 空穴扩散系数hole diffusion coefficient:$D_p$
- 单位时间、单位体积内积累的空穴数
- 少子复合
+单位时间、单位体积内复合recombination的空穴数:$\frac{\Delta p(x,t)}{\tau_p}$ - 非平衡少子寿命$\tau_p$
- 单位时间、单位体积中空穴数的变化
- 非平衡少子(空穴)浓度
- 扩散长度
- 扩散电流密度
外电场E使少子(空穴)产生漂移drift运动
- 漂移电流密度$\mu_p$为空穴迁移率
整流特性
pn结具有单向导电的整流特性,为了推导这一结果,我们假定
- pn结为突变耗尽层,其它区为电中性
- 玻尔兹曼近似
- 载流子小注入
- n区多子majority carrier(电子)浓度(完全电离):$n_{n0}=N_D$
- p区多子(空穴)浓度(完全电离):$p_{p0}=N_A$
- p区少子minority carrier(电子)浓度
$n{p0}=n_i^2/p{
p0}\approx n_{n0} exp(-\frac{eV_D}{k_BT})$
正向电压作用
正向电压$V = V_F> 0$
势垒区内,载流子浓度小、电阻大势垒区外,载流子浓度大、电阻小,电压基本降落在势垒区势垒$x_D$区变窄、变低$e(V_D-V_F)$
破坏平衡,结区漂移运动
结区扩散运动 > 漂移运动
破坏无偏压时的动态平衡
净扩散流,少子正向注入
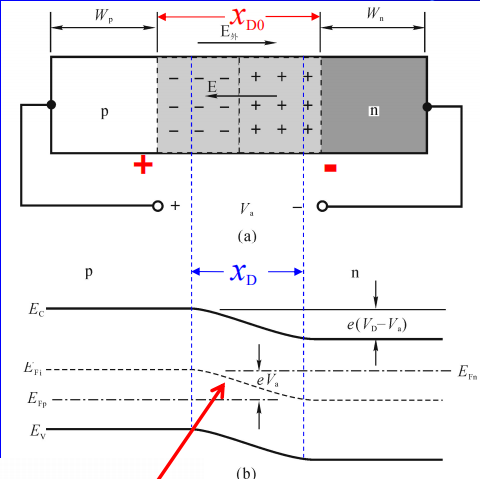
n区,p区中的多子浓度变化不大,但少子浓度会变化几个数量级
- p区电子浓度
- n区空穴浓度
理想二极管方程
反向电流饱和密度
反向电压作用
反偏下,少子浓度很低,少子浓度梯度几乎不随电压变化,达到稳定值
电容特性
势垒电容
pn结的电容效应包括势垒电容和扩散电容两种
击穿特性
反偏电压V增大到$V_B$(击穿电压)
反向电流激烈增大,pn结击穿,击穿
隧道击穿(齐纳击穿Zener breakdown)、
雪崩击穿avalanche breakdown、热电击穿
隧道击穿
p侧价带内电子横穿禁带,直接进入n侧导带内,形成反向电流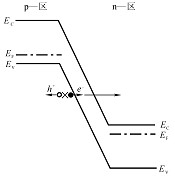
雪崩击穿
- 少子扩散到势垒区
- 少子在势垒区中高速漂移
- 少子从电场获得足够大能量
- 与耗尽区内晶格原子的电子碰
- 产生许多电子—空穴对(二次电子—空穴对)
- 二次电子—空穴对继续漂移、碰撞
- 新的二次电子—空穴对(倍增效应)
- pn结雪崩击穿
隧道效应和雪崩效应主要有载流子浓度决定,
热电击穿
温度升高,平衡少子浓度上升,电流上升,损坏后无法复原
pn二极管
常见的pn结二极管
- 变容二极管
- 开关二极管
- 雪崩二极管
- 隧道二极管
变容二极管
利用反偏pn结电容(势垒电容)随电压非线性变化制成的可变电抗器件
因为势垒电容会随电压变化
理想阶跃结二极管单位面积势垒电容量
线性缓变二极管单位面积势垒电容量
更一般的情况
m = 0,为均匀掺杂结 ;
m = +1,为线性缓变结 ;
m = +2、+3,重掺杂n+ 基片上外延低杂质浓度n层;
m是负值,为超突变结
用途
并联电感,做LC的谐振回路,其震荡频率为:
超突变的谐振频率与反偏电压成正比
开关二极管
利用了二极管正向导通,反向不导通的特性
- t < 0,落在结上正偏压为$V_D$,结两侧扩散区内少子积累,正偏电流为 :
- t =0, 结上压降保持$V_D$不变,反向电流为• $0<t <t_s$反向电流近似恒定扩散区内存储的少子流出被消耗,
结上正偏压逐渐下降到0, $t_s$称为存储时间。 - $t >t_s$,pn结开始反偏,p区和n区内部的少子被反向抽取,空间电荷区增大。
- $t >t_s+ t_2$,pn结稳定, $V_R$电压全落在pn结上,电流为反向饱和电流。
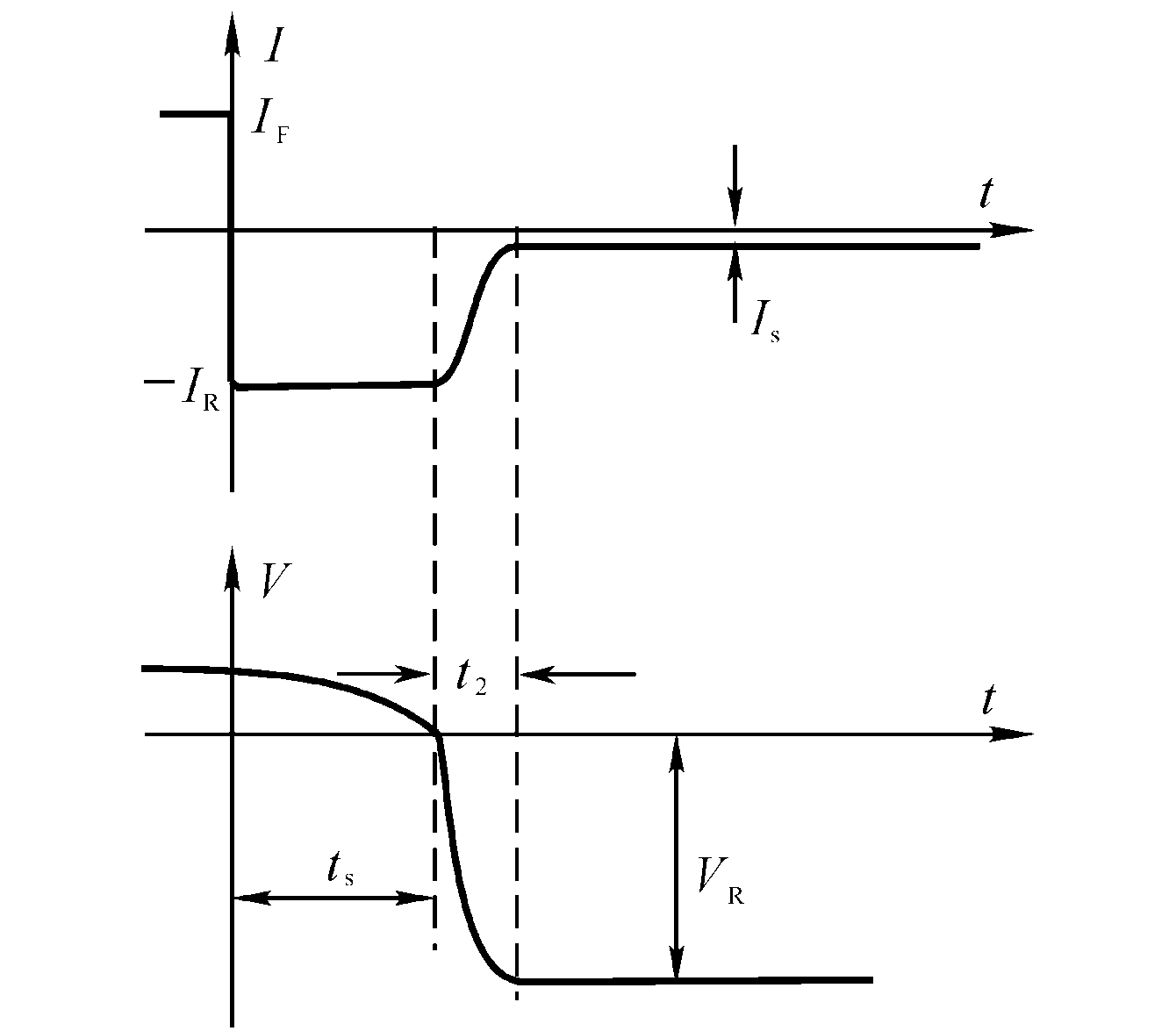
- 反向恢复总时间
隧道二极管
- 隧道二极管是n区,p区都重参杂的pn结二极管,使得n区和p区的费米能级分别进入导带和价带,只有这样的情况才会出现n区导带和p区价带出现相同能量的量子态
- 重掺杂使耗尽区宽度变得很窄,隧道距离很小(约5 ~ 10 nm),提高了隧穿几率。$T \propto epx(-2d)$
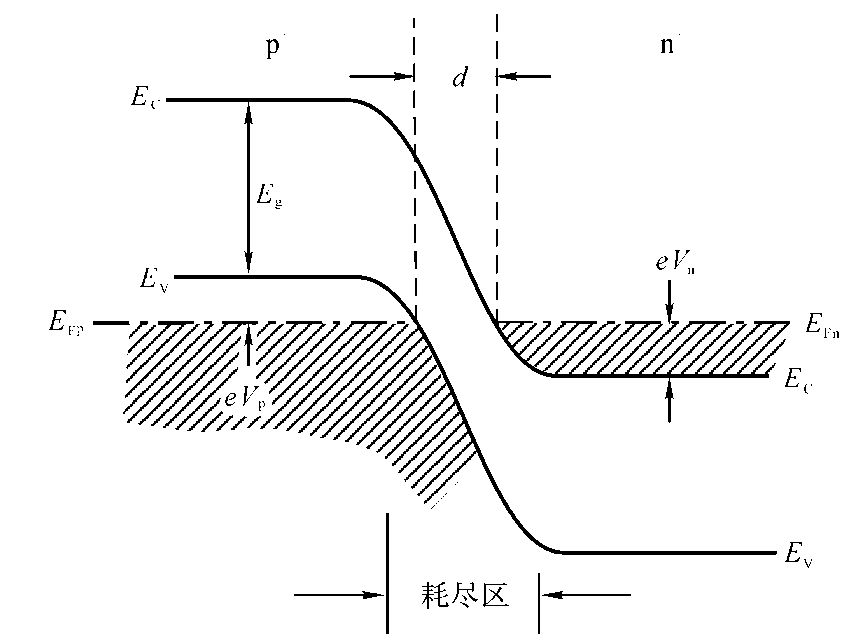
掺杂浓度必须满足以下条件
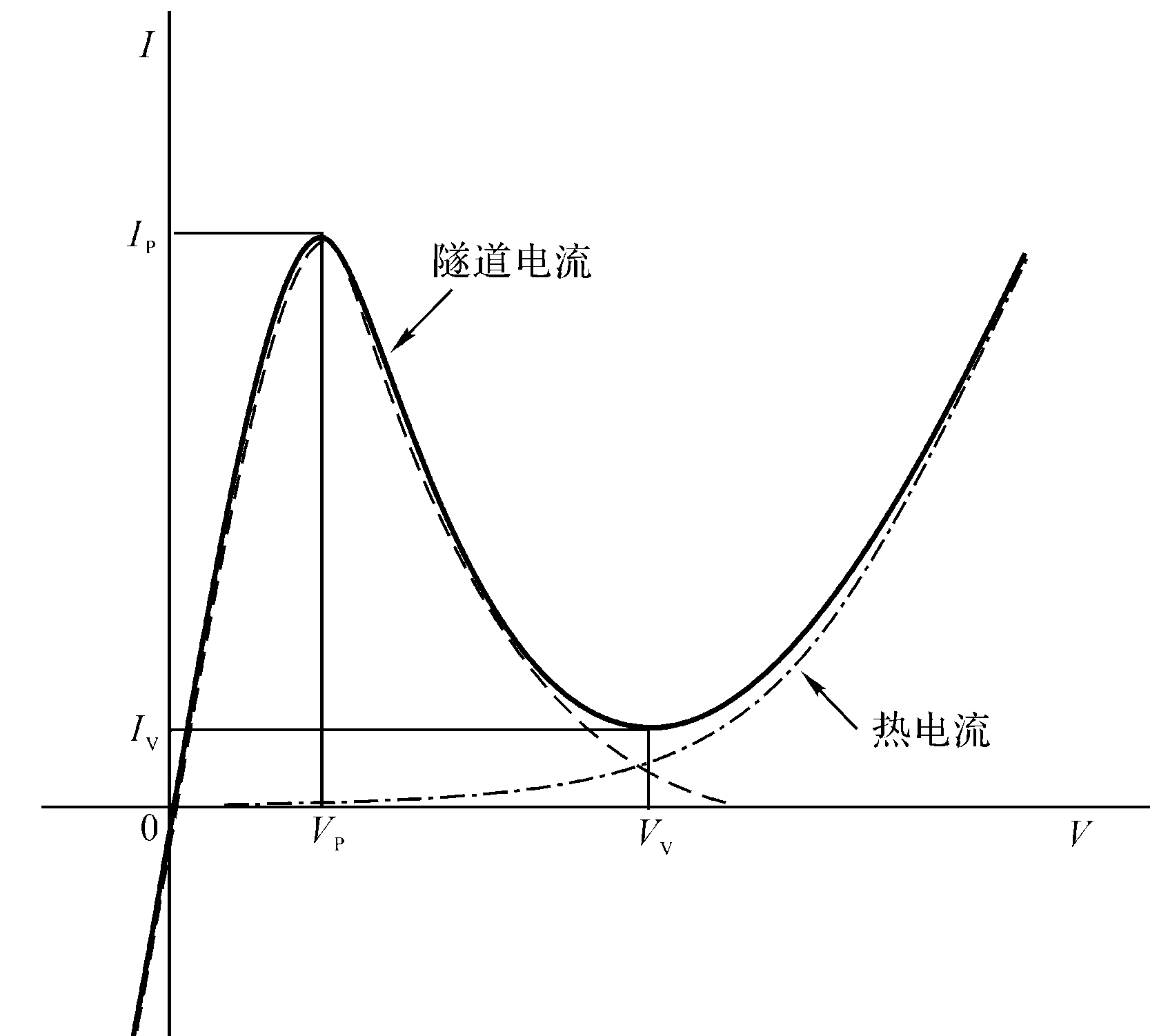
上图展示了隧道二极管电流电压特性的四个阶段
- 隧道效应:n区导带
电子进入p区价带,
产生正向隧道电流 - 隧道效应:n区导带
电子进入p区价带,
产生正向隧道电流 - 隧道效应:n区导带电子
进入p区价带,产生正向
隧道电流,但p区价带顶
介于n区导带底和EF之间 - 只有热电流,
没有隧道效
应产生的隧
道电流
雪崩二极管
雪崩二极管是利用了雪崩效应和渡越效应
微波频率下的负阻效应
双极型晶体管
双极型的晶体管也就是三极管,有pnp和npn两种类型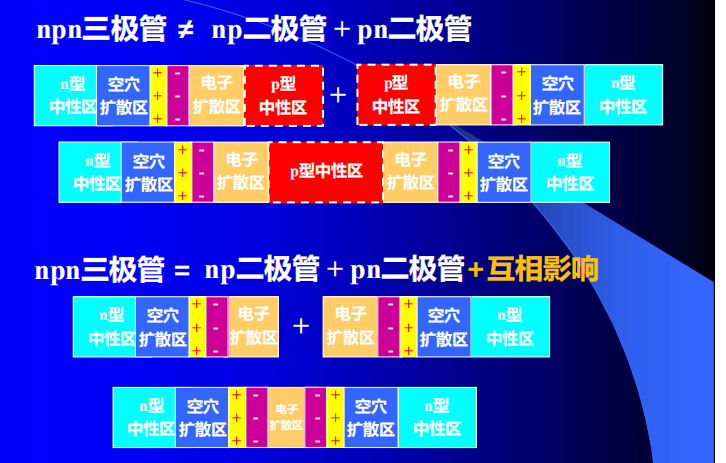
两个背靠背pn结互相影响:基区宽度比少子扩散区短
晶体管噪声
晶体管放大器的主要噪声:
- 外界:输入、感应、耦合等方式引进的噪声
- 晶体管本身:
- 热噪声:载流子无规则热运动引起电流起伏(温度愈
高,热噪声也愈大) - 散粒噪声:载流子数目将在平均值附近起伏
- 低频1/f噪声(1/f):表面能级、晶格缺陷、位错和
晶体不均匀性
- 热噪声:载流子无规则热运动引起电流起伏(温度愈
噪声系数
F = 输入信噪比 / 输出信噪比
金属-半导体和肖特基势垒
金属—半导体(简称金—半或M-S)接触:整流器、检测器、二
极管、场效应晶体管、太阳能电池、半导体集成器件电极
理想肖特基势垒Schottky barrier
- 真空能级$E_0$
电子脱离固体的最小能量(真空能级连续)
- 金属功函数$\phi_m$:
电子从金属中逸出到表
面外的真空中去至少需要的能量。金属费米
能级以上为空态、以下充满电子。
- 半导体功函数$\phi_s$
半导体费米能级与真空能级之差
- 电子亲和势
真空能级与半导体导带底之差 (不变)
真空能级到导带顶部的距离不变
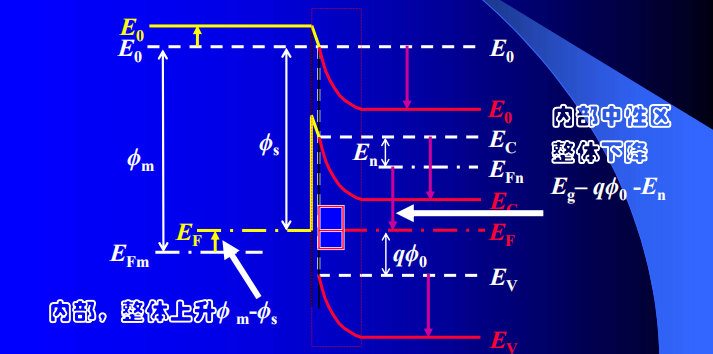
电子会从费米能级高的地方向低处流,所以整个接触过程如下
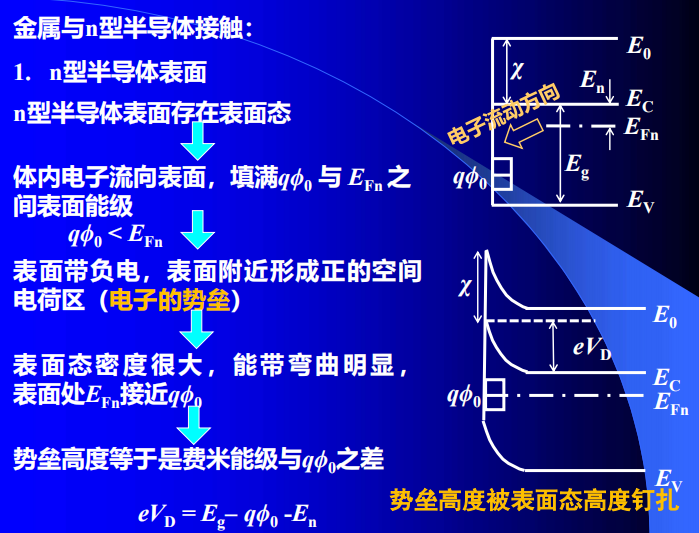
- 电子从半导体流向金属
- 金属表面负电荷、半导体表面带等量正电
- 产生接触电势差(降低/提高了半导体/金属的电子势能)
- 接触电势差阻止半导体中电子继续流向金属
- 平衡状态时 统一的费米能级 没有电子的净流动
接触电势差为
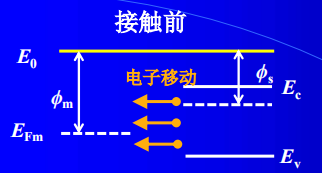
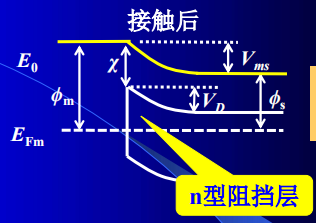
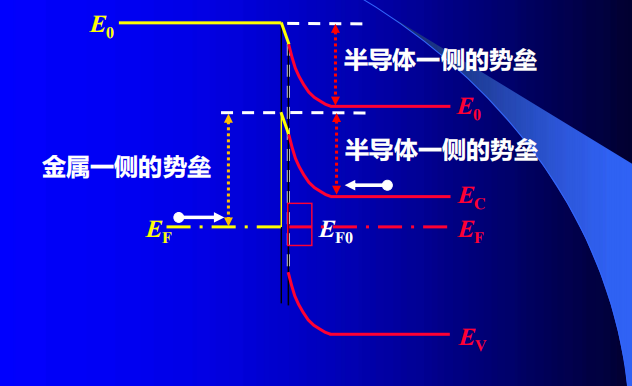
肖特基势垒
- 半导体一侧的势垒高度(电子从半导体进入金属遇到的势垒)
- 金属一侧的势垒(电子从金属进入半导体遇到的势垒)
- 空间电荷区内,电子浓度比内部小得多,形成高阻的区域,
称为阻挡层。
表面态和界面层对接触势垒的影响
- 理想肖特基模型与实验结果不符合:
- 模型:肖特基模型的势垒高度由金属和半导体的功函数决定
- 实验:90%的金属同半导体接触的势垒高度几乎相同,与金属的功函数无关,只与所用半导体的种类相关
- 理想半导体表面(n型半导体)
原子的周期性排列中断,出现半饱和的悬挂键、一些电子能量状态处于面能级(界面态)
表面态一般分为施主型和受主型
- 施主型:能级被电子占据时呈现电中性,施放电子后带正电;
- 受主型:能级空着时呈电中性,接受电子后带负电
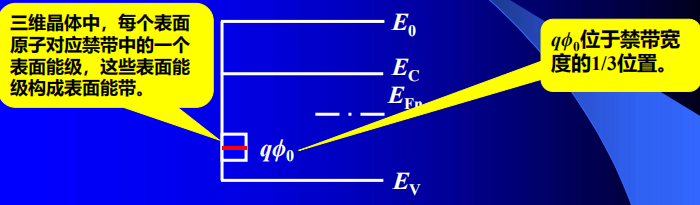
- 电子正好填满$q\phi_0$以下所有的表面态时,表面呈电中性;
- $q\phi_0$以下的表面态空着时,表面带正电,呈施主型。
$q\phi_0$以上的表面态被电子填充时,表面带负电,呈受主型。
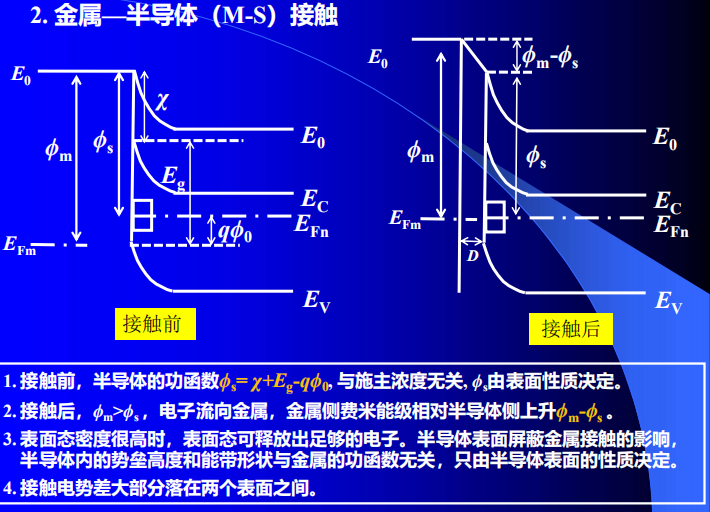
画能带的原则
真空能级$E_0$连续(一般性)
- 电子亲和势$\chi$始终不变$\chi=E_)-E_C$(一般性)
- 费米能级的“钉扎”效应:价带以上$E_g/3$(特殊性)
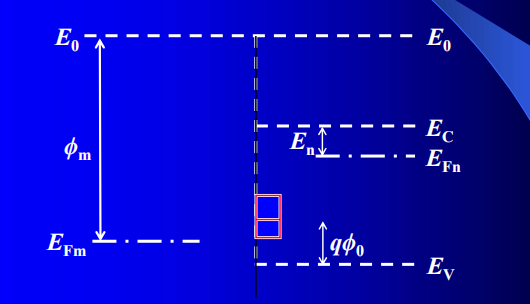
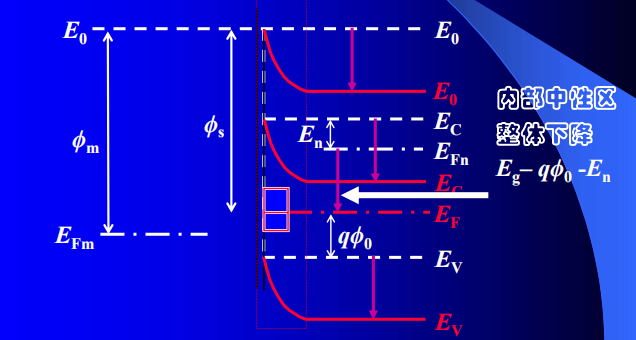
能带草图画法
- 真空能级$E_0$:表面外真空中电子势能(真空能级连续)
- 电子亲和势$\chi$ :真空能级与半导体导带底之差(不变) $\chi = E_0 – E_C$
- 功函数$\phi$ :电子从材料逸出到表面外的真空中,至少需要的能量
$\phi=E_0-E_F$ - 金属功函数$\phim = E_0 – E{Fm}$,金属$E{Fm}$以上为空态、$E{Fm}$以下充满电子
- 半导体功函数$\phi_s = E_0 – E_F$
- 热平衡态,统一的费米能级
- 耗尽层部分能级弯曲
- 中性区(N区、p区)能级不弯曲(有压降除外,例如欧姆接触)
肖特基势垒二极管Schottky barrier diode
肖特基势垒二极管I-V特性与pn结二极管类似
$A^{*}$为有效理查逊常数
肖特基势垒二极管和pn结二极管的特性差异:
- 肖特基势垒二极管为多子越过势垒的热电子发射(微观机理)
thermionic emission of majority carrier - pn结二极管为少子的注入和扩散(微观机理)
diffusion of minority carrier - 反向饱和电流密度特性(宏观特性):
- 肖特基势垒二极管的反向饱和电流密度($10^{-5}A/cm^2 $)
- pn结二极管($10^{-11}A/cm^2 $)
- 开关特性(宏观特性)
肖特基势垒二极管是多子器件,正向偏置时没有扩散电容
(高频特性好,开关时间为ps,pn结二极管为ns) - 肖特基势垒二极管的导通电压比pn结二极管低(宏观特性)
欧姆接触ohmic contact
任何半导体器件或集成电路必须要与外界电学接触,接触电阻由势垒高度、掺杂浓度决定
欧姆接触的势垒有以下两种类型
- 非整流势垒型接触nonrectifying barrier
- 隧道势垒型接触tunneling barrie
场效应晶体管
半导体外加电场时,表面势变化、电阻率变化,在与电场垂直方向的电流变化,所谓场效应,就是垂直的电场控制半导体的导电能力。
场效应晶体管主要有以下几种
- 结型场效应晶体管JFET
- 绝缘栅场效应晶体管IGFET
- (主要是以SiO2作栅极绝缘物的金属Metal—氧化物Oxide—半导体Semiconductor场效应Field-Effect晶体管Transistor: MOSFET)
- 肖特基势垒栅场效应晶体管MESFET
结型场效应晶体管JFET: junction FET
漏极D正偏$V_{DS} > 0$
- $V{DS} < V{DS0}$: $ID$与$V{DS}$接近线性变化
(线性区) - $V{DS0} < V{DS} < V_{DSa}$: $I_D$基本不变化
(饱和区) - $V{DS} > V{DSa}$: ID随VDS急剧增加
(雪崩区)
金属—氧化物—半导体场效应晶体管(MOSFET: metal-oxide-semiconductor FET)
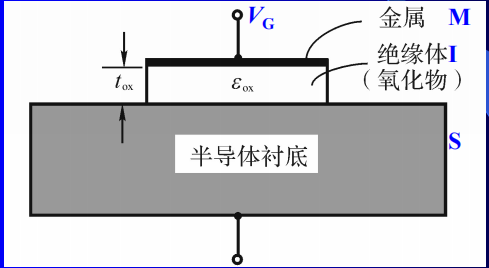
以氧化物作为绝缘层的IGFET,就是金属—氧化物—半导体
场效应管MOSFET
肖特基势垒栅场效应晶体管
(MESFET: metal-semiconductor FET)
肖特基势垒取代JFET的pn结势垒,形成肖特基势垒栅场效应管
异质结及其器件
两种不同半导体材料接触,形成异质结
- 同型isotype(高低)异质结(pP、nN):杂质类型相同
- 异型anisotype(反型)异质结(pN、Pn):杂质类型相反
两种不同材料的禁带宽度,介电系数,晶格常数,热膨胀系数都不同
- 晶格失配率
异质结的能带结构
- 包纳straddling:
- 宽带隙wide-bandgap包纳窄带隙narrow-bandgap
- 交替错开staggered:
- 宽带隙与窄带隙交替错开
- 完全错开broken gap:
- 宽带隙与窄带隙完全错开

- 宽带隙与窄带隙完全错开
异质结特性
理想pN异质结热平衡能带图
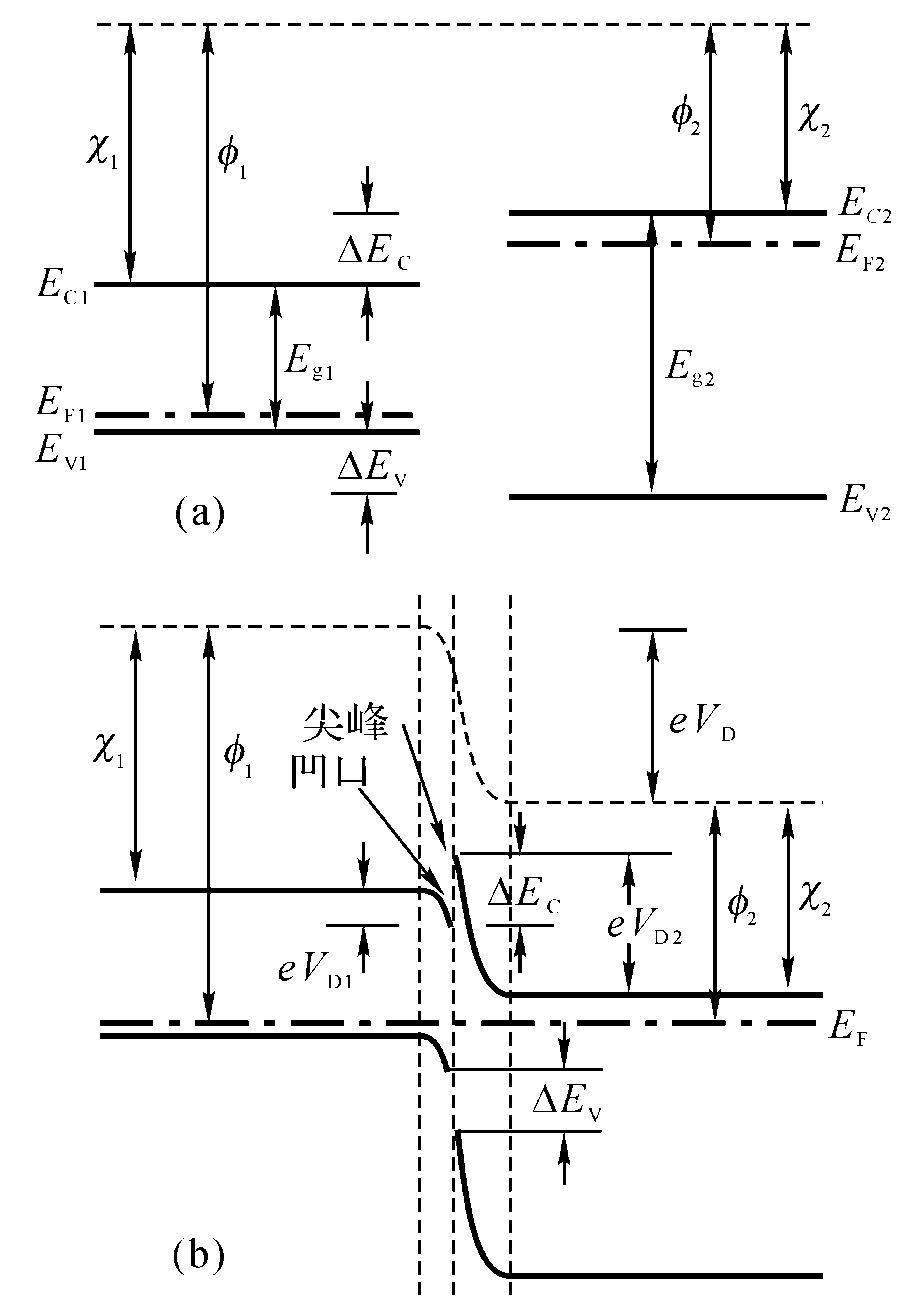
- N区能级向下平移$eV_{D2}$
- p区能级向上平移$eV_{D1}$
