量子力学
不要尝试去理解量子力学!!!
量子力学原理
能量子
- 普朗克常数
黑体辐射
斯特藩-玻尔兹曼定律
总辐出度与温度的四次方成正比
韦恩位移定律
黑体辐射光谱的峰值频率与黑体温度成正比:
波粒二象性
散射增强条件
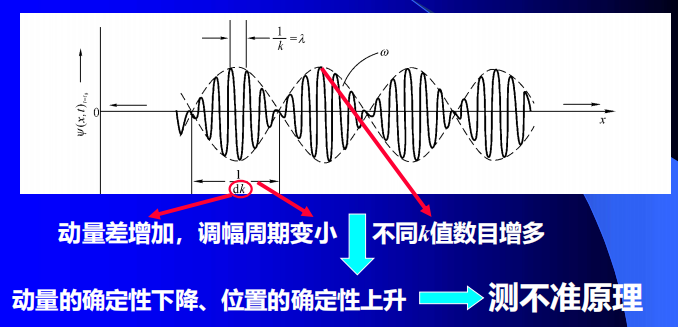
测不准原理
- 动量测不准
- 能量时间测不准
- 角动量测不准
没有人比我更懂量子力学。
薛定谔波动方程
一维非相对论薛定谔方程
对波函数进行变量分离
时间部分为正弦波形式
定态薛定谔方程(与时间无关)
概率密度函数表示在给定时间和位置出现粒子的概率
波函数
粒子在某时刻某位置出现的概率
粒子的几率密度只与位置有关,与时间无关
边界条件
几率密度
- $\psi(r)$有限、单值、连续
动量
各种势场的薛定谔方程的参数往往由边界条件待定
薛定谔方程实例
自由空间中电子
当$U(x)=0$
波函数解为
- 圆频率
- 波数
- 波长
- 动量
无限深势井
当$U(x)_1=0$,$U(x)_2=\infty$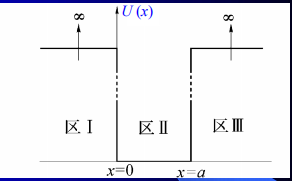
区2
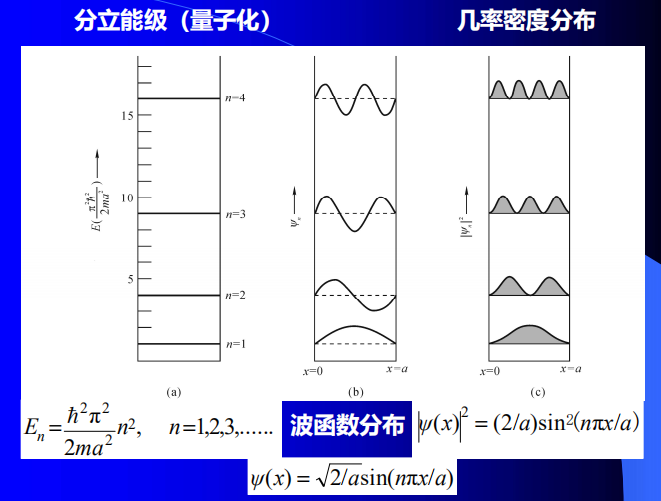
根据边界条件
解得
- 分立能级
阶跃位函数
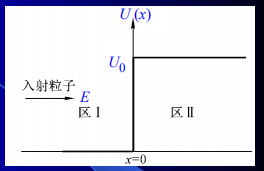
区1
区2
根据边界条件 解得
反射率R=1
粒子有一定几率可以穿越II区,但最终都会掉头返回
势垒
- 区1
- 区2
- 区3
- 透射率
- 反射率
低能量粒子能渗入
或贯穿高能势垒
原子的波动理论
单电子原子
质子和电子产生的位函数
电子的能量
将势函数代入薛定谔方程,并转化为球坐标下进行求解,分离变量可以得到电子的能量
- 电子质量
- 电子电荷量
电子的量子数
- n 主量子数
n=1,2,3… - l 角量子数
l=n-1,n-2…0 - m 磁量子数
|m|=l,l-1…0 - s自旋量子数
s=1/2
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 摸黑干活!
评论
